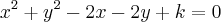passa pelo ponto A(0,1). Sabendo-se que o ponto P pertencente à circunferência mais próximo da origem coincide com o baricentro do triângulo MNQ, onde M(0,k), N(2k,0) e 
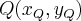é correto afirmar que a área do triângulo MNQ é um número do intervaloGabarito:
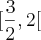
Pessoal, comecei a fazer o seguinte:
1º) Descobri o valor de k = 1, substituindo as coordenadas do ponto k na equação da circunferência dada no início do exercício.
2º) Após isso, achei a seguinte equação da circunferência reduzida:
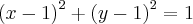
Centro = (1,1) Raio = 1
3º) Achei as coordenadas de M e N, que estavam anteriormente em função de k: M(0,1) e N(2,0)
4º) O exercício falou que o ponto P coincide com o ponto G, que é o baricentro do triângulo MNQ e tal ponto G era pertencente à circunferência e mais próximo da origem. Logo, concluí de que o ponto pertencia a uma reta y = x que passava pela origem e pelo centro (1,1) da circunferência.
5º) Como não tenho as coordenadas do ponto Q, não consigo mais desenvolver o exercício, que acredito eu que para chegarmos ao valor da área devamos fazer uso da fórmula
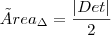
Alguém pode me ajudar? Desde já, agradeço.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.