 por tonycsg2 » Dom Abr 11, 2010 22:14
por tonycsg2 » Dom Abr 11, 2010 22:14
Galera , to quebrando a cabeça aqui não consigo fazer esse exercicio
O Valor de y, para qual e distância do pronto A(1,0) ao ponto B (5,y) seja 5 é :
Me ajudem ,
Brigado .
-
tonycsg2
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Abr 11, 2010 21:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: aministração
- Andamento: cursando
 por lucas92 » Seg Abr 12, 2010 04:18
por lucas92 » Seg Abr 12, 2010 04:18
tonycsg2 escreveu:Galera , to quebrando a cabeça aqui não consigo fazer esse exercicio
O Valor de y, para qual e distância do pronto A(1,0) ao ponto B (5,y) seja 5 é :
Me ajudem ,
Brigado .
Para resolver esse exercício, basta utilizarmos a fórmula da distância entre dois pontos
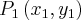
e
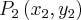
:
![d\left({P}_{1},{P}_{2} \right) = \sqrt[]{\left({x}_{2}-{x}_{1} \right)^2+\left({y}_{2}-{y}_{1} \right)^2} d\left({P}_{1},{P}_{2} \right) = \sqrt[]{\left({x}_{2}-{x}_{1} \right)^2+\left({y}_{2}-{y}_{1} \right)^2}](/latexrender/pictures/90838558ebeee7ebaf54b43048f8917e.png)
Logo, a distãncia entre os pontos
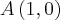
e
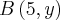
é
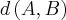
, dada por:
![\sqrt[]{\left(5-1 \right)^2+\left(y-0 \right)^2} = 5 \sqrt[]{\left(5-1 \right)^2+\left(y-0 \right)^2} = 5](/latexrender/pictures/fb8a284fde92b3630cd4b50f6f4a6ef7.png)
![\sqrt[]{4^2+y^2} = 5 \sqrt[]{4^2+y^2} = 5](/latexrender/pictures/36d42d98082feab923fa753a1ec2f6d2.png)
![\sqrt[]{16+y^2} = 5 \sqrt[]{16+y^2} = 5](/latexrender/pictures/dbbf92430d1a27fcbbf2b27da87eb9b5.png)
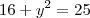
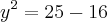
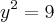

ou
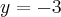
.
-
lucas92
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 09, 2010 06:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda por favor
por zeramalho2004 » Dom Abr 05, 2009 21:31
- 3 Respostas
- 8671 Exibições
- Última mensagem por zeramalho2004

Seg Abr 06, 2009 10:25
Logaritmos
-
- ajuda por favor !!!
por Moacir » Qui Ago 27, 2009 00:19
- 2 Respostas
- 2742 Exibições
- Última mensagem por Moacir

Qui Ago 27, 2009 17:30
Funções
-
- Ajuda Por favor
por Sandy26 » Sex Abr 23, 2010 14:12
- 12 Respostas
- 7154 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Logaritmos
-
- Ajuda, por favor!
por Dimas » Sex Set 24, 2010 23:16
- 2 Respostas
- 1853 Exibições
- Última mensagem por Rogerio Murcila

Qua Set 29, 2010 15:51
Trigonometria
-
- Ajuda por favor.
por Josiebruno » Qua Out 20, 2010 09:36
- 0 Respostas
- 1129 Exibições
- Última mensagem por Josiebruno

Qua Out 20, 2010 09:36
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



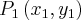 e
e 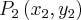 :
:![d\left({P}_{1},{P}_{2} \right) = \sqrt[]{\left({x}_{2}-{x}_{1} \right)^2+\left({y}_{2}-{y}_{1} \right)^2} d\left({P}_{1},{P}_{2} \right) = \sqrt[]{\left({x}_{2}-{x}_{1} \right)^2+\left({y}_{2}-{y}_{1} \right)^2}](/latexrender/pictures/90838558ebeee7ebaf54b43048f8917e.png)
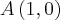 e
e 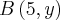 é
é 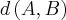 , dada por:
, dada por:![\sqrt[]{\left(5-1 \right)^2+\left(y-0 \right)^2} = 5 \sqrt[]{\left(5-1 \right)^2+\left(y-0 \right)^2} = 5](/latexrender/pictures/fb8a284fde92b3630cd4b50f6f4a6ef7.png)
![\sqrt[]{4^2+y^2} = 5 \sqrt[]{4^2+y^2} = 5](/latexrender/pictures/36d42d98082feab923fa753a1ec2f6d2.png)
![\sqrt[]{16+y^2} = 5 \sqrt[]{16+y^2} = 5](/latexrender/pictures/dbbf92430d1a27fcbbf2b27da87eb9b5.png)
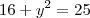
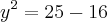
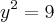
 ou
ou  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.