Sejam ABDC um quadrilátero de vértices A, B, C e D e M, N, P e Q os pontos médios dos lados AB, BD, AC e CD, respectivamente.
(a) Prove que ?
(b) Prove que ?
(c) Prove que MNQP é um paralelogramo.
Se eu assumir que ABDC é quadrado ou retângulo, eu consigo ver que uma diagonal entre seus pontos médios teria a metade do tamanho de uma de suas digonais principais, como por exemplo, no quadrado, Diagonal =
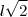e se usar os pontos médios como vértices dos lados, teremos lados com metade do tamanho dos anteriores, com as diagonais dependendo multiplicativamente do lado, um lado com metade do tamanho geraria uma diagonal com metade do tamanho.Entretanto, como eu consigo provar estas 3 afirmativas uma vez que eu nem sei se o quadrilátero ABDC é convexo ou côncavo?
Agradeço pela ajuda.
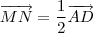
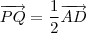
por 
.
