por Larissa28 » Dom Abr 05, 2015 10:03
por adauto martins » Seg Abr 06, 2015 12:34
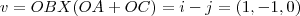
![seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2)](/latexrender/pictures/a1d2c926a7ceed7103f4e906b61c2b62.png "seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2)")
...entao:![v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45°](/latexrender/pictures/cdb2dc20405deb088f6caa6a079e8315.png "v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45°")
por adauto martins » Qui Abr 09, 2015 16:32
por adauto martins » Sex Abr 10, 2015 11:29
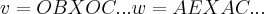sao os vetores normais a esses planos diagonais...entao...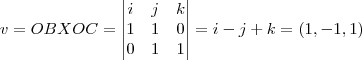
=
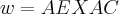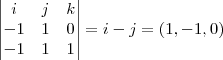,entao...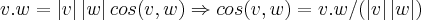
![cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=](/latexrender/pictures/68a2bc55b7507d5a3f69352809cd0c13.png "cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=")
![\Rightarrow (v,w)=arcos(2/\sqrt[]{6})](/latexrender/pictures/52795b8c43a3c54360ce1e469d5a9834.png "\Rightarrow (v,w)=arcos(2/\sqrt[]{6})")
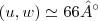
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.