1 - Dado os vértices de um triângulo, A(2,1), B(-1,1) e C (3,2), determine o comprimento da altura relativa ao lado AC. Calcule o comprimento de AC e a área do triângulo.
Aqui minha resolução:
comprimento de AC:
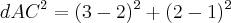
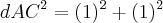
![dAC = \sqrt[]{2} dAC = \sqrt[]{2}](/latexrender/pictures/ec15b3661a431e7698f65322be01a75a.png)
Agora plotando o grafico do triangulo ficaria algo assim:

Para achar a área do triângulo, eu tenho que ter a altura certo, a altura desse triângulo é a distância do ponto C à reta que passa pelos pontos A e B?
Foi isso que eu fiz, achei a equação da reta que passa por A e B:
|-1 1 1 | -1 1
| 2 1 1 | 2 1 = 0
| x y 1 | x y
Resolvendo:
[(-1*1*1) + (1*1*x) + (1*2*y)] - [(1*2*1) + (-1*1*y) + (1*1*x)] = 0
[-1+x+2y] - [2+(-y)+x] = 0
-1 + x + 2y -2 + y - x = 0
3y - 3 = 0 (eq. geral da reta q passa por A e B) -> Essa eq. pode ter x nulo?
Agora fazendo a distancia entre o ponto C e a eq. da reta que passa por A e B, para achar a altura:
![d = \frac{|0*3 + 3*2 +(-3)|}{\sqrt[]{0^2 + 3^2}} d = \frac{|0*3 + 3*2 +(-3)|}{\sqrt[]{0^2 + 3^2}}](/latexrender/pictures/6209f83a3bcfdde3e58c058ed6190b1c.png)
d = 1, logo h = 1
Agora achando a base, que seria a distancia de B a A?
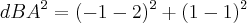
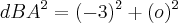
![dBA = \sqrt[]{9} dBA = \sqrt[]{9}](/latexrender/pictures/251c16895bab238b1a1f63b00b95450c.png)
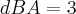
logo base = 3
Agora fazendo a área:
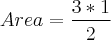
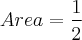
E agora como achar a altura relativa ao lado AC?


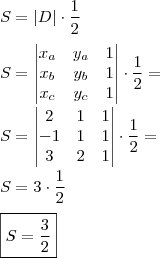
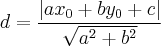 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.