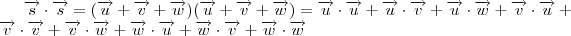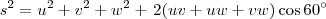por Nicolas1Lane » Dom Mar 23, 2014 00:33
por Nicolas1Lane » Dom Mar 23, 2014 00:33
A questão quer que se encontre a partir de uma relação aonde o s=u+v+w sendo que u, v e w formam dois a dois ângulos de 60º e ainda que o módulo de u é 4, o de v é 3 e finalmente w igual a 1. Determinar então o módulo do vetor s. Que deve dar raiz de 35.
O que eu tentei até agora foi usar a relação de ângulo entre 2 vetores com ângulo teta 60º para pegar o resultado já que eu já tinha alguns módulos. Mas o modo como tenho os dados me deixaram incerto de como prosseguir corretamente.
s=u+v+w pensei em substituir nesta relação os módulos, mas não encontrei sentido nesta ideia e como não tenho vetor algum fica um pouco mais complicado.
Eu já estou tentando a tarde inteira nesta questão e nada do que resolvo fecha com a que supostamente deveria.
Será que poderiam me ajudar ao menos como trabalhar esta relação com o ângulo para eu fazer o resto. Estou simplesmente perdido já que o que tentei até agora não resultou no esperado.
-
Nicolas1Lane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Set 11, 2013 23:25
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Exatas/Ciência da Computação
- Andamento: cursando
 por Russman » Dom Mar 23, 2014 18:58
por Russman » Dom Mar 23, 2014 18:58
Basta você lembrar que
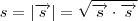
Como
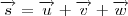
, então
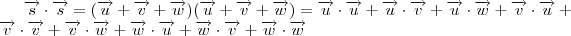
que simplifica-se-a ,dada configuração dos vetores,
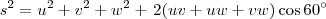
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Nicolas1Lane » Dom Mar 23, 2014 19:13
por Nicolas1Lane » Dom Mar 23, 2014 19:13
Muito obrigado mesmo.
-
Nicolas1Lane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Set 11, 2013 23:25
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Exatas/Ciência da Computação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Encontrar a reta t
por -civil- » Ter Ago 09, 2011 21:49
- 1 Respostas
- 2213 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 23:31
Geometria Analítica
-
- [geometria analítica e calculo vetorial] modulo de um vetor
por Suellem Albuquerque » Sex Mar 28, 2014 15:36
- 0 Respostas
- 1175 Exibições
- Última mensagem por Suellem Albuquerque

Sex Mar 28, 2014 15:36
Geometria Analítica
-
- [Geometria Analítica] Encontrar a eq. vetorial da reta
 por -civil- » Qua Ago 10, 2011 16:16
por -civil- » Qua Ago 10, 2011 16:16
- 3 Respostas
- 2451 Exibições
- Última mensagem por LuizAquino

Qui Ago 18, 2011 10:15
Geometria Analítica
-
- [Geometria Analítica] Encontrar os vértices do hexágono
 por -civil- » Qua Ago 10, 2011 16:51
por -civil- » Qua Ago 10, 2011 16:51
- 1 Respostas
- 2091 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 12:44
Geometria Analítica
-
- [Geometria Espacial] Encontrar os lados dos triângulos
 por rochadapesada » Ter Abr 16, 2013 19:40
por rochadapesada » Ter Abr 16, 2013 19:40
- 3 Respostas
- 3028 Exibições
- Última mensagem por young_jedi

Qua Abr 17, 2013 20:51
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


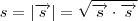
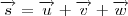 , então
, então