 por marysuniga » Qui Dez 19, 2013 16:02
por marysuniga » Qui Dez 19, 2013 16:02
Como eu posso fazer este exercício:
Mostre que, se
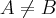
, então (A,B) e (B,A) são de mesmo comprimento, mesma direção e sentido contrário.
Obrigada
-
marysuniga
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Dez 19, 2013 15:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
 por e8group » Dom Jan 05, 2014 16:42
por e8group » Dom Jan 05, 2014 16:42
Talvez é um pouco tarde . Lá vai algumas dicas .Para provar que

e
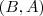
possuem comprimento iguais ,a mesma direção e sentido opostos é suficiente mostrar que
(i) Os segmentos geométricos
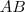
e
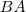
possuem mesmo comprimento .
(ii)

e
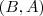
são colineares ( ambos estão contidos em uma mesma reta)
(iii) Os segmentos geométricos
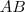
e
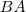
tem interseção não vazia ,
respectivamente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marysuniga » Seg Jan 06, 2014 13:32
por marysuniga » Seg Jan 06, 2014 13:32
Não foi tarde não, valeu!!

-
marysuniga
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Dez 19, 2013 15:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Segmento AB
 por gustavowelp » Sex Nov 19, 2010 09:42
por gustavowelp » Sex Nov 19, 2010 09:42
- 1 Respostas
- 1653 Exibições
- Última mensagem por Pedro123

Sex Nov 19, 2010 12:26
Sistemas de Equações
-
- Medida de um segmento
por flavio2010 » Sex Jul 09, 2010 09:04
- 1 Respostas
- 1763 Exibições
- Última mensagem por Tom

Sex Jul 09, 2010 09:24
Álgebra Elementar
-
- Medida do segmento
por Balanar » Dom Ago 29, 2010 18:40
- 1 Respostas
- 2768 Exibições
- Última mensagem por MarceloFantini

Seg Ago 30, 2010 01:23
Álgebra Elementar
-
- Mediatriz de um segmento
por ARCS » Sex Abr 22, 2011 13:11
- 1 Respostas
- 14918 Exibições
- Última mensagem por NMiguel

Sex Abr 22, 2011 13:46
Geometria Analítica
-
- O valor do segmento PQ
 por maria cleide » Qui Out 13, 2011 11:52
por maria cleide » Qui Out 13, 2011 11:52
- 1 Respostas
- 1223 Exibições
- Última mensagem por maria cleide

Sex Out 14, 2011 22:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
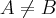 , então (A,B) e (B,A) são de mesmo comprimento, mesma direção e sentido contrário.
, então (A,B) e (B,A) são de mesmo comprimento, mesma direção e sentido contrário.
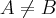 , então (A,B) e (B,A) são de mesmo comprimento, mesma direção e sentido contrário.
, então (A,B) e (B,A) são de mesmo comprimento, mesma direção e sentido contrário.
 e
e 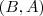 possuem comprimento iguais ,a mesma direção e sentido opostos é suficiente mostrar que
possuem comprimento iguais ,a mesma direção e sentido opostos é suficiente mostrar que 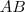 e
e 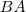 possuem mesmo comprimento .
possuem mesmo comprimento . e
e 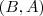 são colineares ( ambos estão contidos em uma mesma reta)
são colineares ( ambos estão contidos em uma mesma reta)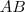 e
e 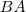 tem interseção não vazia ,
tem interseção não vazia ,




 , avisa que eu resolvo.
, avisa que eu resolvo.

