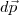em coordenadas retangulares é: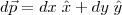
E em coordenadas polares é:
Mas a minha dúvida é o seguinte: o vetor de posição
para a localização de um ponto P com coordenas (x, y) ou (r, ?), em coordenadas retangulares é:
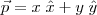
Mas e em coordenadas polares, seria este:
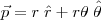
ou este:
ou outro? Qual?
por