Bom dia!
Esta questão é de um concurso.
Num plano cartesiano, uma circunferência de equação x² + y² + ax+ by= 24 passa pelos pontos (2,2) e (4,0). Pode-se afirmar que o centro da circunferência está no
(A) primeiro quadrante, e o raio é maior do que 1.
(B) primeiro quadrante, e o raio é menor do que 1.
(C) terceiro quadrante, e o raio é menor do que 1.
(D) terceiro quadrante, e o raio é maior do que 1.
(E) quarto quadrante, e o raio é maior do que 1.
Não estou conseguindo montar a equação da circunferência. Pensei em começar pela distância entre pontos mas também não deu certo, pois é exatamente o que pede o enunciado.
Obrigada


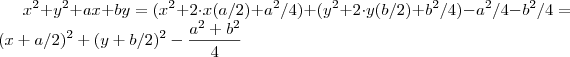 .
. 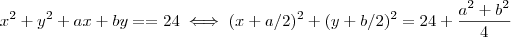 .
.
 Acho que preciso de mais uma dica
Acho que preciso de mais uma dica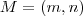 este ponto e suponha
este ponto e suponha 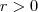 (fixo) a distancia dos pontos equidistantes de
(fixo) a distancia dos pontos equidistantes de 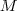 .Então um ponto
.Então um ponto 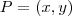 pertence a esta circunferência , sse
pertence a esta circunferência , sse 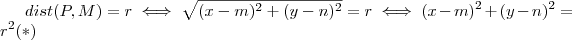 .
.  com
com 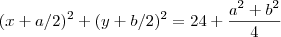 temos :
temos : 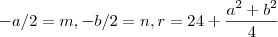 .Assim ,
.Assim , 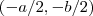 é
é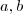 utilize os dois pontos dados .Tente concluir e comente as dúvidas .
utilize os dois pontos dados .Tente concluir e comente as dúvidas .
 .
.
 :
: