 por Mariana111 » Seg Out 26, 2009 17:30
por Mariana111 » Seg Out 26, 2009 17:30
Me ajudem a resolver esses problemas por favor ! :
Primeiro problema -> Em um triângulo retângulo ABC , a diferença entre os catetos é 2 cm e o produto é 48 cm² . Calcule :
a) a hipotenusa deste triângulo
b) a altura relativa a hipotenusa .
c) as projeções dos catetos sobre a hipotenusa .
Segundo problema -> Na rua da esquina existia um poste com 5 metros de altura . Num dia de tempestade , o poste tombou embatendo numa janela que se encontra a um terço da altura do prédio onde morava João . Sabendo que a distância do poste ao edifício é de 2 metros , calcule a altura do prédio em causa.
obrigada.
-
Mariana111
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 26, 2009 17:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Seg Out 26, 2009 18:51
por Cleyson007 » Seg Out 26, 2009 18:51
Boa noite!
Seja bem vinda ao Ajuda Matemática!
Mariana, vou ser bem breve... tenho aula daqui a pouco.
Quanto a letra a: Monte o sistema de equações:


Resolvendo o sistema, você encontrará os valores de b e c. Para achar o valor da hipotenusa, jogue no teorema de Pitágoras:
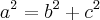 Quanto a letra b:
Quanto a letra b: A altura relativa à hipotenusa pode ser encontrada, usando a fórmula:
 Quanto a letra c:
Quanto a letra c:As projeções podem ser encontradas usando as fórmulas:


Depois respondo a segunda questão.

Comente qualquer dúvida.

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Mariana111 » Seg Out 26, 2009 18:59
por Mariana111 » Seg Out 26, 2009 18:59
a letra a não consigo entender quando faço c-b=2 e cb=48 como eu resolvo isso e o que eu faço depois ?
-
Mariana111
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 26, 2009 17:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Mariana111 » Seg Out 26, 2009 19:14
por Mariana111 » Seg Out 26, 2009 19:14
Muito obrigada pela ajuda da 1ª questão ! =)
-
Mariana111
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 26, 2009 17:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Seg Out 26, 2009 20:23
por Molina » Seg Out 26, 2009 20:23
Mariana111 escreveu:a letra a não consigo entender quando faço c-b=2 e cb=48 como eu resolvo isso e o que eu faço depois ?
Confirma Mariana, já conseguiu entender o procedimento?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em teorema de pitagoras
 por tadeutato » Sáb Abr 30, 2011 15:37
por tadeutato » Sáb Abr 30, 2011 15:37
- 1 Respostas
- 1116 Exibições
- Última mensagem por FilipeCaceres

Sáb Abr 30, 2011 15:51
Geometria Plana
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4685 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3523 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1933 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12668 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




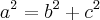









 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.