estava estudando as interseções de planos y = k no parabolóide hiperbólico de equação
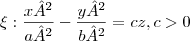
e neste material de estudo, dizia que essa interseção seria a parábola
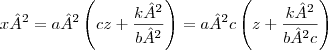
de retas focais paralelas ao eixo -OZ, vértice no ponto
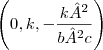 e concavidade voltada para cima, para
e concavidade voltada para cima, para 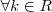 , uma vez que a²c é < 0...
, uma vez que a²c é < 0...minha dúvida é entender como ele achou o vértice dessa parábola. podem me dar uma força?
obrigado e abraços!!


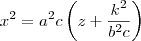
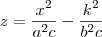

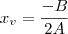
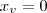
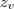 é so substituir o valor de x
é so substituir o valor de x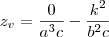
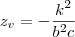

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)