 por MrJuniorFerr » Sáb Out 13, 2012 18:11
por MrJuniorFerr » Sáb Out 13, 2012 18:11
Estou com dúvida no seguinte exercício:
Escreva uma equação do plano paralelo ao eixo z e que contém os pontos A(2,0,0) e B(0,3,2) Gabarito:
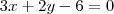
Resolvi da seguinte forma:
Como o plano é paralelo ao eixo z, sabe-se que o vetor
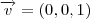
é pertencente ao plano, mas no meu ponto de vista, este (0,0,1) também é um ponto pertencente ao plano, então usei C(0,0,1). Portanto agora tenho 3 pontos pertencentes ao plano.
Fazendo
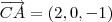
e
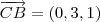
, encontro 2 vetores coplanares e não colineares. Portanto,

X
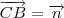
Após fazer o produto escalar dos 2 vetores, obtive que
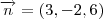
Fazendo
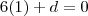
, encontro

Enfim, substituindo, a equação geral do plano que encontrei foi
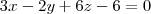
.
Alguém sabe me explicar o por quê do meu resultado estar diferente do gabarito e se a minha resolução está certa?
Obrigado
Edit:
Aproveitando o tópico, qual a diferença quando um plano é definido pelo eixo z ou o plano é paralelo ao eixo z?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Sáb Out 13, 2012 20:48
por young_jedi » Sáb Out 13, 2012 20:48
o ponto C(0,0,1) não é pertencente o plano, voce tem que o vetor v=(0,0,1) é paralelo ao plano portanto os dois vetore que voce tem para achar a equação do plano são

e
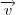
fazendo o produto vetorial entre os dois voce encontra um vetor normal ao plano e com isso consegue determinar o plano
Um plano definido pelo exio z, é um plano que contem o exio z ou seja, qualquer ponto do tipo (0,0,z) pertence ao plano
ja um ponto paralelo ao eixo isso não ocorre, oque ocorre é que qualquer vetor do tipo (0,0,z) é paralelo ao plano, mais os pontos do tipo (0,0,z), não peretence ao plano.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Sáb Out 13, 2012 20:50
por MarceloFantini » Sáb Out 13, 2012 20:50
Seu resultado está diferente do gabarito porque está errado. Um plano ser paralelo ao eixo

significa que o vetor normal ao plano é ortogonal ao vetor diretor do eixo. Logo o vetor normal do plano será da forma
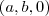
e a equação geral do plano
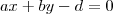
.
Substituindo os pontos temos
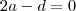
e
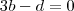
. O que o gabarito fez foi simplesmente facilitar a vida e tomar

, de onde segue que

e

, tornando a equação do plano
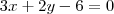
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação de planos] Dúvida exercício
por MrJuniorFerr » Sáb Out 06, 2012 17:16
- 2 Respostas
- 3847 Exibições
- Última mensagem por MrJuniorFerr

Sáb Out 06, 2012 18:19
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 2
por MrJuniorFerr » Sáb Out 06, 2012 20:39
- 14 Respostas
- 8624 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 19:07
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 3
por MrJuniorFerr » Dom Out 07, 2012 02:49
- 3 Respostas
- 2200 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 17:21
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 4
por MrJuniorFerr » Seg Out 08, 2012 07:40
- 1 Respostas
- 1250 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 10:06
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 5
por MrJuniorFerr » Qui Out 11, 2012 08:58
- 4 Respostas
- 1976 Exibições
- Última mensagem por MrJuniorFerr

Qui Out 11, 2012 12:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
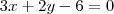
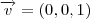 é pertencente ao plano, mas no meu ponto de vista, este (0,0,1) também é um ponto pertencente ao plano, então usei C(0,0,1). Portanto agora tenho 3 pontos pertencentes ao plano.
é pertencente ao plano, mas no meu ponto de vista, este (0,0,1) também é um ponto pertencente ao plano, então usei C(0,0,1). Portanto agora tenho 3 pontos pertencentes ao plano.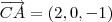 e
e 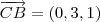 , encontro 2 vetores coplanares e não colineares. Portanto,
, encontro 2 vetores coplanares e não colineares. Portanto,  X
X 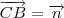
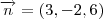
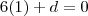 , encontro
, encontro 
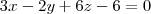 .
.

 e
e 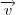
 significa que o vetor normal ao plano é ortogonal ao vetor diretor do eixo. Logo o vetor normal do plano será da forma
significa que o vetor normal ao plano é ortogonal ao vetor diretor do eixo. Logo o vetor normal do plano será da forma 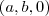 e a equação geral do plano
e a equação geral do plano 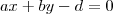 .
.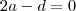 e
e 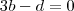 . O que o gabarito fez foi simplesmente facilitar a vida e tomar
. O que o gabarito fez foi simplesmente facilitar a vida e tomar  , de onde segue que
, de onde segue que  e
e  , tornando a equação do plano
, tornando a equação do plano 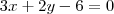 .
.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.