felipe10 escreveu:Gostaria de ajuda com a seguinte questão...
Seja um vetor v = (2,-1,1), obter:
- um vetor unitário ortogonal ao vetor v
- um vetor de módulo 4 ortogonal aovetor v
Eu acho o vetor unitário, mas não ortogonal ao vetor v.... Se alguem puder me ajudar... grato...
Primeiro você precisa notar que existem infinitas respostas para esse exercício.
Desejamos que um vetor
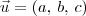
seja ortogonal ao vetor
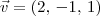
. Isso significa que devemos ter
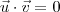
. Ou seja, devemos ter que 2a - b + c = 0.
Escolhendo um valor para b e c, podemos obter um valor para a. Obviamente vamos escolher valores simples. Por exemplo, se b = 2 e c = 0, temos que a = 1.
Desse modo, o vetor
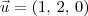
é um dos possíveis vetores que é ortogonal a

.
Agora basta usar esse vetor
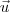
para encontrar os dois vetores solicitados no exercício:
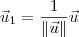
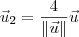
Tente continuar a partir daí.


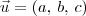 seja ortogonal ao vetor
seja ortogonal ao vetor 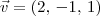 . Isso significa que devemos ter
. Isso significa que devemos ter 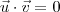 . Ou seja, devemos ter que 2a - b + c = 0.
. Ou seja, devemos ter que 2a - b + c = 0. 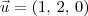 é um dos possíveis vetores que é ortogonal a
é um dos possíveis vetores que é ortogonal a  .
.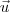 para encontrar os dois vetores solicitados no exercício:
para encontrar os dois vetores solicitados no exercício: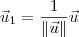
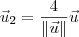


 .
.
 :
: