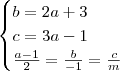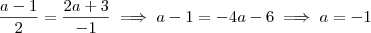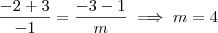manuoliveira escreveu:Calcular o valor de m para que as retas r e s sejam coplanares:
r: y = 2x + 3 e z = 3x - 1
s: (x-1)/2 = y/(-1) = z/m
Você precisa começar determinando os vetores diretores das retas.
Um vetor diretor de s é fácil perceber que é

.
Já para perceber o vetor diretor de r, vamos fazer x = t e montar as seguintes equações paramétricas:
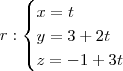
Desse modo, um vetor diretor para a reta r será
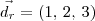
.
Note que para qualquer valor de m, sempre os vetores
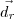
e
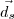
terão direções diferentes. Portanto, as retas r e s podem ser: reversas ou concorrentes.
Se elas forem reversas, então elas não são coplanares.
Mas se elas forem concorrentes, então elas serão complanares. Esse é o caso que nos interessa.
Ora, para que elas sejam concorrentes deve haver um ponto de interseção. Ou seja, deve existir um ponto P = (a, b, c) tal que:
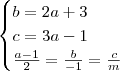
Substituindo b e c na terceira equação, ficamos com:

Considerando a primeira parte dessa equação, temos que:
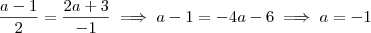
Considerando agora a última parte dessa equação, já substituindo a = -1, temos que:
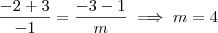
Portanto, para m = 4 teremos as retas r e s complanares e concorrentes, sendo que o ponto de interseção será P = (-1, 1, -4).



 .
.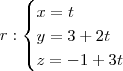
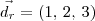 .
.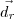 e
e 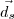 terão direções diferentes. Portanto, as retas r e s podem ser: reversas ou concorrentes.
terão direções diferentes. Portanto, as retas r e s podem ser: reversas ou concorrentes.