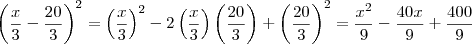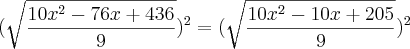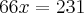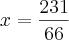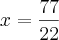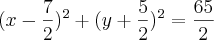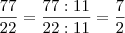por Claudin » Sáb Mai 05, 2012 16:21
por Claudin » Sáb Mai 05, 2012 16:21
Determine a equação da circunferência que contém os pontos
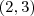
e

e tem centro na reta

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Mai 05, 2012 19:04
por LuizAquino » Sáb Mai 05, 2012 19:04
Claudin escreveu:Determine a equação da circunferência que contém os pontos
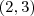
e

e tem centro na reta

Se o centro C da circunferência está nessa reta, então temos que
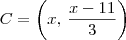
.
Como A = (2, 3) e B = (-1, 1) são pontos dessa circunferência, então a distância deles para o centro C é a mesma (e é igual ao raio).
Temos então que:
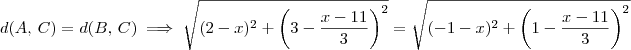
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Mai 05, 2012 22:10
por Claudin » Sáb Mai 05, 2012 22:10
Encontrei um resultado incoerente
Poderia me ajudar?
Cheguei até
![\sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}} \sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}}](/latexrender/pictures/28e4f17db53b14530a644c4727938845.png)
Extrai a raiz, e acabei achando um valor negativo para x.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sáb Mai 05, 2012 22:14
por Claudin » Sáb Mai 05, 2012 22:14
Fiz novamente e encontrei um resultado também inadequado, parece.
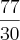
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 06, 2012 09:18
por LuizAquino » Dom Mai 06, 2012 09:18
Claudin escreveu:Encontrei um resultado incoerente
Poderia me ajudar?
Cheguei até
![\sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}} \sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}}](/latexrender/pictures/28e4f17db53b14530a644c4727938845.png)
Extrai a raiz, e acabei achando um valor negativo para x.
Refaça suas contas, pois você deveria encontrar:
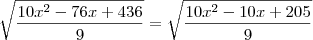
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 06, 2012 09:50
por Claudin » Dom Mai 06, 2012 09:50
![\sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2} \sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2}](/latexrender/pictures/199cef608dbeffbf196f181db887bded.png)
![\sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2} \sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2}](/latexrender/pictures/d1291eb60e2c7bed60100c51ced2d393.png)
![\sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2} \sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2}](/latexrender/pictures/7a50c3a6bc83bc981ccf1472c5deaa8a.png)
até aqui tudo certo?
Já refiz várias vezes e não encontro resultado.
Se puder me ajudar ai...
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 06, 2012 10:36
por LuizAquino » Dom Mai 06, 2012 10:36
Claudin escreveu:![\sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2} \sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2}](/latexrender/pictures/199cef608dbeffbf196f181db887bded.png)
![\sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2} \sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2}](/latexrender/pictures/d1291eb60e2c7bed60100c51ced2d393.png)
![\sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2} \sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2}](/latexrender/pictures/7a50c3a6bc83bc981ccf1472c5deaa8a.png)
até aqui tudo certo?
Já refiz várias vezes e não encontro resultado.
A terceira linha está correta, mas na segunda você apenas cometeu um erro de digitação. No primeiro membro, note que no lugar de -1 o correto seria -3.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 06, 2012 10:41
por Claudin » Dom Mai 06, 2012 10:41
![\sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})} \sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})}](/latexrender/pictures/9ababdc4128405948fd0a23cb7ce1a46.png)
Acho então que meu erro deve esta a partir desse ponto
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Mai 06, 2012 11:02
por Claudin » Dom Mai 06, 2012 11:02
Eu achava que ficaria
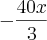
e
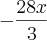
?
O resto do desenvolvimento do produto notável sobre 9, o meu
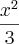
foi erro de digitação mesmo.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 06, 2012 11:08
por LuizAquino » Dom Mai 06, 2012 11:08
Claudin escreveu:Eu achava que ficaria
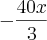
e
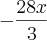
?
Obviamente não fica. Note, por exemplo, que:
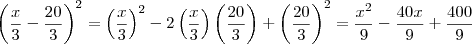
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 06, 2012 11:59
por Claudin » Dom Mai 06, 2012 11:59
LuizAquino escreveu:Refaça suas contas, pois você deveria encontrar:
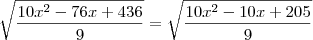
Agora tente continuar a partir daí.
Consegui chegar até aqui.
Logo depois elevei ambos os membros ao quadrado
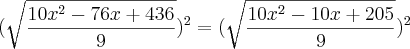

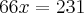
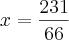
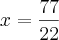
O que achei meio estranho, pois no caso encontrei o raio
Sendo que a resposta seria
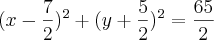
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Mai 06, 2012 14:35
por Claudin » Dom Mai 06, 2012 14:35
Claro, claro, que desatenção.
Obrigado pela ajuda Luiz.
To com umas dúvidas em propagação de erros, cálculos de incertezas de amostras, posso postar isso no tópico de conversão de unidades, pois envolve isso também?

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1884 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Circunferência
por ilovemat » Sex Abr 03, 2009 19:12
- 5 Respostas
- 9515 Exibições
- Última mensagem por Marcampucio

Seg Abr 06, 2009 20:11
Trigonometria
-
- circunferência
por jeffersonricardo » Seg Set 06, 2010 15:20
- 7 Respostas
- 4362 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 17:14
Geometria Analítica
-
- circunferencia
 por cosme » Qua Nov 17, 2010 09:29
por cosme » Qua Nov 17, 2010 09:29
- 2 Respostas
- 1833 Exibições
- Última mensagem por MarceloFantini

Qua Nov 17, 2010 15:11
Trigonometria
-
- Circunferência
por Pri Ferreira » Qua Nov 09, 2011 21:02
- 1 Respostas
- 1310 Exibições
- Última mensagem por LuizAquino

Qui Nov 10, 2011 20:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
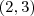 e
e  e tem centro na reta
e tem centro na reta 

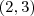 e
e  e tem centro na reta
e tem centro na reta 

e
e tem centro na reta
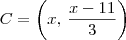 .
.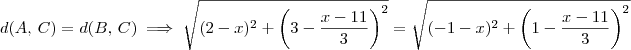

![\sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}} \sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}}](/latexrender/pictures/28e4f17db53b14530a644c4727938845.png)

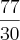

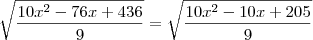

![\sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2} \sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2}](/latexrender/pictures/199cef608dbeffbf196f181db887bded.png)
![\sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2} \sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2}](/latexrender/pictures/d1291eb60e2c7bed60100c51ced2d393.png)
![\sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2} \sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2}](/latexrender/pictures/7a50c3a6bc83bc981ccf1472c5deaa8a.png)


![\sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})} \sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})}](/latexrender/pictures/9ababdc4128405948fd0a23cb7ce1a46.png)

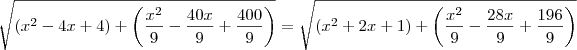

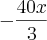 e
e 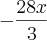 ?
?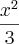 foi erro de digitação mesmo.
foi erro de digitação mesmo.
e
?