ramahk escreveu:Dados os vetores OA = [1 2 -2], OB = [3 0 1],e OC = [2 3 -3], pede-se:
a) Calcule a altura relativa h ao vértice C do paralelogramo formado pelos vetores AB e AC;
b) A área a do paralelogramo.
ramahk escreveu:a)
AB = OA - OB => [-2 2 -3] (chamei de vetor a)
AC = OA - OC => [-1 -1 1] (chamei de vetor b)
Essas subtrações não fazem sentido. O correto seria:
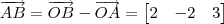
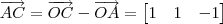
ramahk escreveu:Por Pitágoras: a² * cos² D + h² = a²
dai vem: h² = 17 * sen² D;
Isso que você escreveu não faz sentido. Se
a é um vetor, você não pode escrever
a². Não está definida a operação de potenciação entre vetores.
A figura abaixo ilustra o exercício.
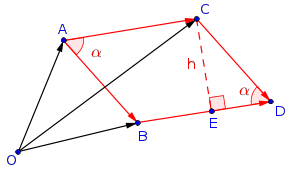
- figura.png (6.84 KiB) Exibido 667 vezes
Aplicando o Teorema de Pitágoras no triângulo CDE, temos que:
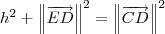
Note o uso dos módulos. Como o módulo é um escalar (um número), podemos elevá-lo ao quadrado.
Continuando, temos que:

e
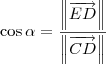
. Sendo assim, podemos escrever que:
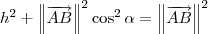
ramahk escreveu:como ainda não aprendi produto interno, não da pra usar a desigualdade de Cauchy e não consigo sair daqui...
Mesmo que você já tivesse estudado a
Desigualdade de Cauchy-Schwarz, não faria sentido tentar aplicar uma
desigualdade nesse exercício.
Se você já tivesse estudado o produto interno, então bastava aplicar a relação:
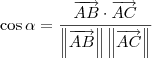
Mas já que você ainda não estudou isso, a saída é aplicar a
Lei dos Cossenos no triângulo ABC. Desse modo, temos que:
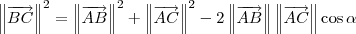
Nessa equação, você já sabe quanto vale
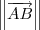
e
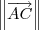
. Falta determinar o valor de
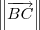
. Para determinar esse valor, lembre-se que
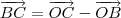
. Por fim, depois que você determinar aquele módulo a única coisa que fica faltando na equação é

. Ou seja, com essa equação você pode determinar o valor de

. A partir disso fica fácil determinar o valor de h.
ramahk escreveu:b) Área do paralelogramo = ||a|| * ||b|| = sqrt (17*3).
Errado. A área
S do paralelogramo será:
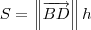
Lembrando que

, podemos dizer que a área será:
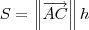
Agora tente terminar o exercício.


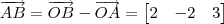
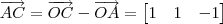
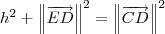
 e
e 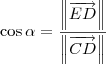 . Sendo assim, podemos escrever que:
. Sendo assim, podemos escrever que: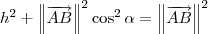
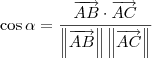
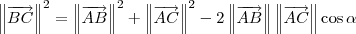
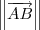 e
e 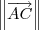 . Falta determinar o valor de
. Falta determinar o valor de 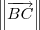 . Para determinar esse valor, lembre-se que
. Para determinar esse valor, lembre-se que 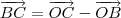 . Por fim, depois que você determinar aquele módulo a única coisa que fica faltando na equação é
. Por fim, depois que você determinar aquele módulo a única coisa que fica faltando na equação é  . Ou seja, com essa equação você pode determinar o valor de
. Ou seja, com essa equação você pode determinar o valor de 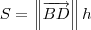
 , podemos dizer que a área será:
, podemos dizer que a área será: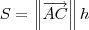


 .
.
 :
: