 por Claudin » Qua Nov 02, 2011 03:19
por Claudin » Qua Nov 02, 2011 03:19
Se U, V e W são vetores tais que V x U = V x W e V diferente do vetor nulo, então U = V.
Designei V = (Va, Vb, Vc)
W = (Wa, Wb, Wc)
U = (Ua, Ub, Uc)
Sendo assim "abri" todos os produtos vetoriais propostos no exercício, e resultou em:
(Vb.Uc - Va.Ub)i, (Vc.Ua - Va.Uc)j, (Va.Ub - Vb.Ua)k ------> V x U
(Vb.Wc - Vc.Wb)i, (Vc.Wa - Va.Wc)j, (Va.Wb - Vb.Wa)k -----> V x W
Sendo assim substituindo U = W, os resultados seriam iguais.
Mas o correto agora seria atribuir valores numéricos aos vetores U, V e W? Para ver se realmente a alternativa é verdadeira?
Mas ela é falsa, e devido a essas contas acima não conseguir provar corretamente o falso, e sim o contrário.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Nov 06, 2011 17:43
por LuizAquino » Dom Nov 06, 2011 17:43
Claudin escreveu:Se U, V e W são vetores tais que V x U = V x W e V diferente do vetor nulo, então U = V.
Eu presumo que o final da afirmação é: "(...)
então U = W".
Essa afirmação é falsa.
Quando temos uma afirmação falsa, basta exibir um contraexemplo.
Escolha
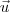
e
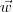
distintos e paralelos a

. Nesse caso irá ocorrer
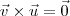
e
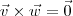
. Ou seja, teremos
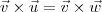
, mas
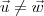
.
Exemplo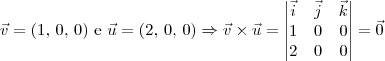
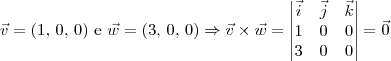
Portanto,
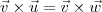
, mas
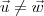
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7372 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2996 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5216 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3409 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2387 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


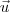 e
e 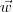 distintos e paralelos a
distintos e paralelos a  . Nesse caso irá ocorrer
. Nesse caso irá ocorrer 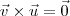 e
e 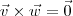 . Ou seja, teremos
. Ou seja, teremos 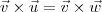 , mas
, mas 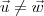 .
.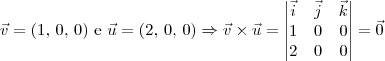
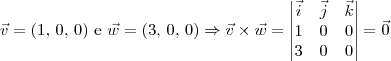
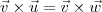 , mas
, mas 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
