Se U, V e W são vetores tais que V x U = V x W e V diferente do vetor nulo, então U = V.
Designei V = (Va, Vb, Vc)
W = (Wa, Wb, Wc)
U = (Ua, Ub, Uc)
Sendo assim "abri" todos os produtos vetoriais propostos no exercício, e resultou em:
(Vb.Uc - Va.Ub)i, (Vc.Ua - Va.Uc)j, (Va.Ub - Vb.Ua)k ------> V x U
(Vb.Wc - Vc.Wb)i, (Vc.Wa - Va.Wc)j, (Va.Wb - Vb.Wa)k -----> V x W
Sendo assim substituindo U = W, os resultados seriam iguais.
Mas o correto agora seria atribuir valores numéricos aos vetores U, V e W? Para ver se realmente a alternativa é verdadeira?
Mas ela é falsa, e devido a essas contas acima não conseguir provar corretamente o falso, e sim o contrário.


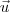 e
e 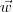 distintos e paralelos a
distintos e paralelos a  . Nesse caso irá ocorrer
. Nesse caso irá ocorrer 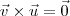 e
e 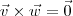 . Ou seja, teremos
. Ou seja, teremos 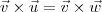 , mas
, mas 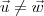 .
.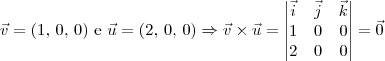
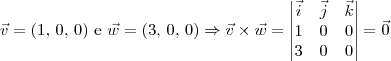
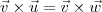 , mas
, mas 

 .
.



