Considere o paralelepípedo que tem um dos vértices no ponto A = (2, 2, 4) e os três vértices adjacentes a A nos pontos B = (7, 0, 7), C= (-3, 4, 6) e D= (1, 1, 12).
a) Determine as coordenadas do vértice E oposto ao vértice A.
Teria que traçar os possíveis vetores? AB, AC, AD, BC?
O que seriam os vértices adjacentes a A? Seriam os demais vértices?
b)Calcule a área da face que contém os pontos A, B, C.
Seria o produto vetorial de AB e AC?
c) Calcule o volume do paralelepípedo.
Iria calcular utilizando o produto misto entre três vetores correto?
Alguém ajudaria esclarecendo essas dúvidas, mostrando o caminho a ser seguido e se possível uma prévia resolução, pois necessito de saber como resolver o exercício com urgência, pois minha prova é depois de amanha e ainda continuo com essa dúvida.


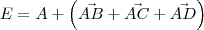
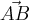 e
e 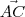 . Isto é, deve-se calcular
. Isto é, deve-se calcular 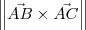 .
.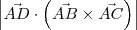 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
