18-17) Considere as retas r: X= (1,1,0) +
 (0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano
(0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano  , e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos:
, e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos:(a)
 : x - y + z = 2
: x - y + z = 2Fazendo a intersecção de s e
 , encontrei o ponto A = (2,
, encontrei o ponto A = (2,  ,
,  )
)Fazendo a intersecção entre r e Oxz
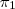 : X = (0,0,0) +
: X = (0,0,0) +  (1,0,0) +
(1,0,0) +  (0,01)
(0,01)1 =

1 +
 = 0
= 0 =
= 
 = -1,
= -1,  = -1,
= -1,  = 1
= 1B = (1, 0, -1)
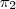 : X = (0,0,0) +
: X = (0,0,0) +  (1,0,0) +
(1,0,0) +  (0,1,0)
(0,1,0)1 =

1 +
 = 0
= 0 = 0
= 0 C = (1,1,0)
Usando os três pontos para calcular o determinante, cheguei que o determinante é igual a 2 e a área será 1. Mas o resultado do livro é
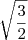 . O que tem de errado na minha resolução.
. O que tem de errado na minha resolução.

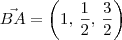
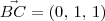
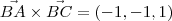 .
.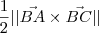 .
.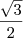 .
.

 .
.
 :
: