18-9) O segmento BE é a base de um triângulo isósceles de vértice A e é também a intersecção desse triângulo com o retângulo de vértices B, C, D, E. Os cinco pontos são coplanares. Conhecendo A = (1,1,0), B = (2,0,1) e C = (6,-2,3), obtenha as coordenadas de D e E (SO).
Como o triângulo ABE é isóceles, cada ângulo interno tem 60º.
Considerando E = (
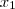 ,
, 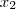 ,
, 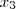 )
)||
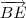 ||.||
||.||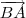 ||. cos 60º =
||. cos 60º = 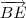 .
.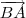
3.
 = ( - 2,
= ( - 2, 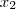 ,
, 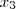 - 1).(-1,1,-1)
- 1).(-1,1,-1)1)
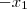
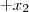
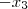 +
+  = 0
= 0dist(B,A) =
 =
=  = dist (B,E)
= dist (B,E)dist(B,E) =
 =
= 
2) (
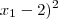 + (
+ (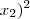 + (
+ (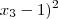 = 3
= 3Como consigo encontrar mais equações para achar essas incógnitas do ponto E?


 ;
; e
e 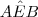 são congruentes.
são congruentes.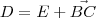 .
.
 é o plano formado por A, B e C
é o plano formado por A, B e C = (1,-1,1) e
= (1,-1,1) e 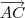 = (5,-3,3)
= (5,-3,3) (1,-1.1) +
(1,-1.1) +  (5,-3,3)
(5,-3,3) ,
,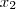 ,
,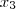 )
)
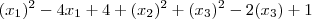
 = ||
= ||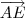 ||.||
||.||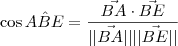 .
.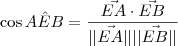 .
.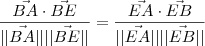 . Como
. Como  , no final ficamos com
, no final ficamos com  . Vamos chamar essa equação de (3).
. Vamos chamar essa equação de (3).![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)