-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480645 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542060 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 505783 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 734230 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2178273 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por willwgo » Qui Fev 17, 2011 16:31
por willwgo » Qui Fev 17, 2011 16:31
ola estou começando a estudar esta materia agora estou com algumas duvidas e alguns problemas para resolver alguns exercicios!
o principal e esse!
Resolva a equaçao abaixo:
A-
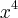
-2x³ + x² + 2x - 2=0,sabendo que duas de suas raizes são -1 e 1.
B- x³ - 7x² + 36 =0 ,sabendo que -2 é uma de suas raizes.
se alguem consiguir resolver me explique passo a passo de como chegaram ao resultado!
desde ja agradeço!
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qui Fev 17, 2011 16:43
por DanielFerreira » Qui Fev 17, 2011 16:43
Resolva a equaçao abaixo:
A- -2x³ + x² + 2x - 2=0,sabendo que duas de suas raizes são -1 e 1.
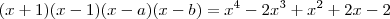
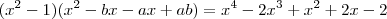

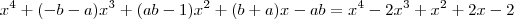
- b - a = - 2 ========> a = - b + 2
ab - 1 = 1 ==========> ab = 2
b(- b + 2) = 2
- b² + 2b = 2
b² - 2b + 2 = 0
delta = 4 - 8
delta = - 4
delta = 4i²


Editado pela última vez por
DanielFerreira em Qui Fev 17, 2011 17:03, em um total de 1 vez.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qui Fev 17, 2011 16:54
por DanielFerreira » Qui Fev 17, 2011 16:54
B- x³ - 7x² + 36 =0 ,sabendo que -2 é uma de suas raizes.
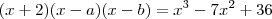
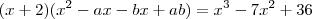
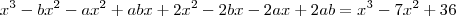
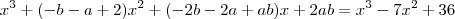
- b - a + 2 = - 7 =============> a + b = 9
- 2b - 2a + ab = 0 ===========> 2a + 2b = ab
2ab = 36 ==================> ab = 18
achemos dois números cuja soma é 9 e o produto seja 18.
3 e 6portanto, (x + 2)(x - 3)(x - 6)
R = {- 2, 3, 6}
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equaçoes] me ajudem com estes 2 exercicios
por teilom » Dom Ago 04, 2013 17:18
- 1 Respostas
- 1945 Exibições
- Última mensagem por Fernanda Almeida

Dom Ago 04, 2013 19:42
Equações
-
- É possível alguém resolver estes exercícios de Limite?
por adam » Sex Jul 12, 2013 14:25
- 5 Respostas
- 2723 Exibições
- Última mensagem por adam

Dom Jul 14, 2013 13:19
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo resolver esta questão, por favor me ajudem!
por Derlan » Ter Jul 04, 2017 15:32
- 0 Respostas
- 1724 Exibições
- Última mensagem por Derlan

Ter Jul 04, 2017 15:32
Geometria Analítica
-
- função linear, me ajudem a achar estes pontos m,y,b
por teilom » Qui Mar 19, 2015 23:31
- 0 Respostas
- 1413 Exibições
- Última mensagem por teilom

Qui Mar 19, 2015 23:31
Álgebra Elementar
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 2737 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
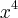 -2x³ + x² + 2x - 2=0,sabendo que duas de suas raizes são -1 e 1.
-2x³ + x² + 2x - 2=0,sabendo que duas de suas raizes são -1 e 1.

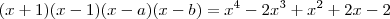
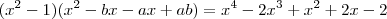

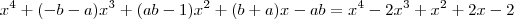



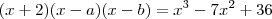
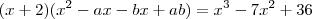
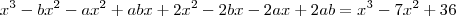
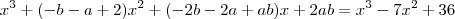


 , avisa que eu resolvo.
, avisa que eu resolvo.

