 por Rose » Sex Set 21, 2012 18:42
por Rose » Sex Set 21, 2012 18:42
Boa tarde!!
Estou com duvida nesta questão: Verifique se o polinômio p(x)= 2x^5 + 23x^4 + 96x^3 + 162 x^2 + 54x - 81 possui alguma raiz real de multiplicidade 4, e caso possua, encontre-a.
Resolução
Não sei se entendi certo o problema mas dividi o p(x)= 2x^5 + 23x^4 + 96x^3 + 162 x^2 + 54x - 81 por ( x-4) e obtive como resultado : q(x)= 2x^4 + 31x^3 +220x^2+ 1042 x + 4222 e r (x) =16880...Com isso conclui que X- 4 não é raiz....Mas como encontrar a riz certa!! Podes me ajudar!!
-
Rose
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qui Mai 15, 2008 14:13
- Área/Curso: Estudante
- Andamento: cursando
 por young_jedi » Sex Set 21, 2012 19:59
por young_jedi » Sex Set 21, 2012 19:59
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Sex Set 21, 2012 23:56
por MarceloFantini » Sex Set 21, 2012 23:56
Jedi, por que escreveu

? Uma raíz de multiplicidade quatro quer dizer que

, então estou perguntando por que da mudança de notação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por young_jedi » Sáb Set 22, 2012 10:08
por young_jedi » Sáb Set 22, 2012 10:08
Voce esta certo MarceloFantini, obrigado por conferir, foi apenas um descuido meu
o correto é isto mesmo que vc colocou.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7160 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Raízes de polinômio
por ARCS » Ter Jan 25, 2011 21:46
- 1 Respostas
- 3104 Exibições
- Última mensagem por Renato_RJ

Ter Jan 25, 2011 22:33
Álgebra Elementar
-
- Raizes de um polinomio de grau 3
por Lilavet » Qua Abr 28, 2010 09:42
- 2 Respostas
- 5704 Exibições
- Última mensagem por DeMoNaZ

Qua Abr 28, 2010 18:25
Polinômios
-
- Fatoração e raízes de um polinômio
por pablohas » Qua Dez 08, 2010 21:26
- 2 Respostas
- 3767 Exibições
- Última mensagem por Elcioschin

Sex Dez 10, 2010 22:05
Polinômios
-
- Cálculo das raízes de um polinômio
por eu_dick1 » Ter Nov 11, 2014 23:42
- 0 Respostas
- 1605 Exibições
- Última mensagem por eu_dick1

Ter Nov 11, 2014 23:42
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


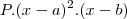
 é sua raiz de multiplicidade quatro e b é uma raiz de multiplicidade 1
é sua raiz de multiplicidade quatro e b é uma raiz de multiplicidade 1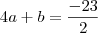
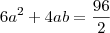
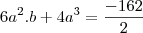
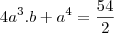

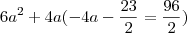

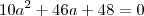
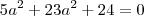
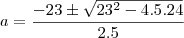
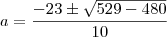
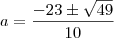
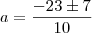

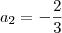
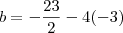
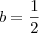

 ? Uma raíz de multiplicidade quatro quer dizer que
? Uma raíz de multiplicidade quatro quer dizer que  , então estou perguntando por que da mudança de notação.
, então estou perguntando por que da mudança de notação.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.