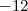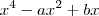Pessoal, o problema é o seguinte: O polinômio
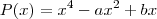 é divisível por x+3 e o resto de sua divisão por x-1 é a abcissa do ponto médio do segmento MN, onde M(-9,3) e N(-15,-4).Encontre os valores de a e b.
é divisível por x+3 e o resto de sua divisão por x-1 é a abcissa do ponto médio do segmento MN, onde M(-9,3) e N(-15,-4).Encontre os valores de a e b.Bem, primeiro resolvi P(x) por x+3 pelo dispositivo de Briot-Ruffini e que deu um resultado nada satisfatório, então depois tirei a raiz de x+3=0 => x=-3
e fiz
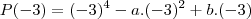 e cheguei a P(-3)= 81- 9a -3b. E daí em diante não consegui resolver o problema e nem aplicar os conceitos de geometria analítica.
e cheguei a P(-3)= 81- 9a -3b. E daí em diante não consegui resolver o problema e nem aplicar os conceitos de geometria analítica.Por favor, alguém me ajude nessa questão!!!



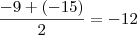
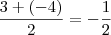
 tem resto igual a
tem resto igual a