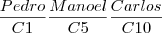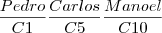por joaofonseca » Sáb Mai 05, 2012 10:00
por joaofonseca » Sáb Mai 05, 2012 10:00
Numa sala de aula existem 3 filas de mesas, cada fila com 10 cadeiras.Ao distribuir 30 alunos pelos 30 lugares,qual a probabilidade de um grupo de 3 amigos ficarem na mesma fila?
Os casos possíveis serão iguais a 30!
A minha dúvida está nos casos favoráveis.
O gabarito é
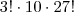
A meu ver, por cada arranjo que os 3 amigos ocuparem em cada fila, os restantes alunos podem permutar 27! formas diferentes nas restantes 27 cadeiras. Ora os 3 amigos podem sentar-se em cada fila de A(10,3)=720 maneiras diferentes. Não consigo entender o gabarito!
Alguém me pode ajudar?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Fabiano Vieira » Sáb Mai 05, 2012 11:20
por Fabiano Vieira » Sáb Mai 05, 2012 11:20
joaofonseca escreveu:Ora os 3 amigos podem sentar-se em cada fila de A(10,3)=720 maneiras diferentes. Não consigo entender o gabarito!
Se três amigos sentam-se em três cadeiras, eles poderão sentar-se de 6(3!) modos diferentes nessas mesmas cadeiras. Exemplo:
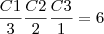
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por joaofonseca » Dom Mai 06, 2012 07:29
por joaofonseca » Dom Mai 06, 2012 07:29
Fabiano Vieira , não entendi a tua resposta.Podes clarificar?
Contudo realso que os três amigo se podem sentar em 10 cadeiras possíveis e a ordem conta. e ainda que existem 3 filas entre as quaos os amigos podem escolher uma.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Fabiano Vieira » Dom Mai 06, 2012 12:47
por Fabiano Vieira » Dom Mai 06, 2012 12:47
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por joaofonseca » Dom Mai 06, 2012 20:00
por joaofonseca » Dom Mai 06, 2012 20:00
Fabiano Vieira , o teu raciocinio estaria correto se só existissem 3 cadeiras.Mas existem 10(em cada fila). Por isso eles podem sentar-se noutras cadeiras.
Agora pensando, o 1º amigo tem à disposição 10 cadeiras para se sentar, o 2º amigo só terá 9 cadeiras e o 3º amigo terá 8 cadeiras onde se sentar. Assim, em cada fila, os amigos podem sentar-se
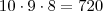
. Ou seja é uma premutação
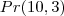
.
Contudo existem 3 filas, logo existem
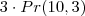
. Mas como a ordem conta, a posição de cada um dos restantes 27 alunos é importante. Por isso por cada posição que os 3 amigos ocupem nas diferentes filas, os restantes alunos podem permutar
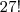
.
Os casos favoráveis serão
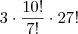
. Só posso concluir que o gabarito está errado!!!!!!!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Fabiano Vieira » Dom Mai 06, 2012 23:43
por Fabiano Vieira » Dom Mai 06, 2012 23:43
joãofonsenca,
Mesmo se eles sentarem em cadeiras diferentes na mesma fila, ainda sim eles poderão sentar de seis maneiras diferentes.
Ex:
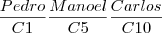
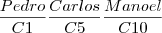
...e seguindo o mesmo exemplo já feito.
Mas como a questão fala de probabilidade e não maneiras diferentes, concordo com você. Porque, acho, o fato deles sentarem de seis maneiras diferentes nessas mesmas cadeiras não alterara o resultado.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo combinatorio
por joaofonseca » Seg Jan 16, 2012 23:18
- 1 Respostas
- 1891 Exibições
- Última mensagem por fraol

Seg Jan 16, 2012 23:56
Desafios Difíceis
-
- Notação Calculo Combinatorio
por joaofonseca » Qua Jan 11, 2012 20:36
- 3 Respostas
- 1975 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 11, 2012 21:49
Estatística
-
- DILEMA COMBINATÓRIO!
por jorge1986 » Qua Jul 01, 2009 11:23
- 4 Respostas
- 4096 Exibições
- Última mensagem por jorge1986

Qua Jul 29, 2009 15:39
Estatística
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6491 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
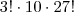


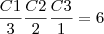

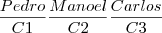
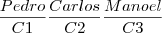
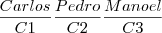
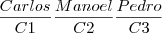
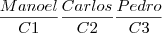
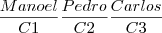
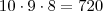 . Ou seja é uma premutação
. Ou seja é uma premutação 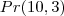 .
.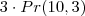 . Mas como a ordem conta, a posição de cada um dos restantes 27 alunos é importante. Por isso por cada posição que os 3 amigos ocupem nas diferentes filas, os restantes alunos podem permutar
. Mas como a ordem conta, a posição de cada um dos restantes 27 alunos é importante. Por isso por cada posição que os 3 amigos ocupem nas diferentes filas, os restantes alunos podem permutar 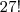 .
.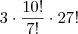 . Só posso concluir que o gabarito está errado!!!!!!!
. Só posso concluir que o gabarito está errado!!!!!!!