Você deve evitar aplicar a distributiva. Isso só dificulta a solução da inequação.
Vejamos como proceder.
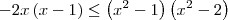
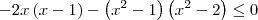
Usando o produto notável
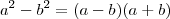
, temos que:
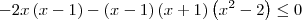
Colocando o termo (x-1) em evidência, temos que:
![\left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0 \left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0](/latexrender/pictures/38338842c9b7f4edd0afa4158423fbd8.png)
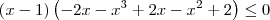
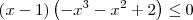
Aqui você precisa fatorar um polinômio de grau 3. Se você ainda não sabe como fazer isso, então é recomendado que você faça uma revisão.
Para fatorar esse polinômio, precisamos descobrir as suas raízes. Uma delas é fácil de obter. Note que se x = 1, temos que
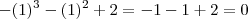
. Ou seja, x = 1 é uma raiz desse polinômio. Para achar as outras, precisamos aplicar um processo de redução de grau. Tipicamente, esse processo é realizado aplicando-se o dispositivo prático de Briot-Ruffini. Após a aplicação desse processo, você deve obter:
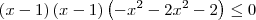
Agora basta resolver essa inequação produto.
Se você ainda não sabe como resolver algo desse tipo, eu recomendo que você consulte o material abaixo.
Inequação Produto - Brasil Escolahttp://www.brasilescola.com/matematica/ ... duto-1.htmMatemática - Aula 9 - Inequações - Parte 5Canal do Nerckie no YouTube:
http://www.youtube.com/nerckie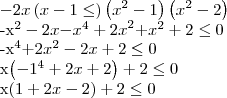

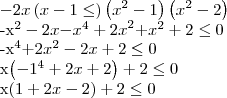

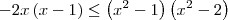
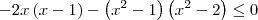
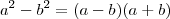 , temos que:
, temos que: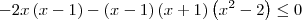
![\left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0 \left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0](/latexrender/pictures/38338842c9b7f4edd0afa4158423fbd8.png)
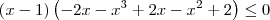
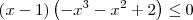
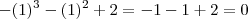 . Ou seja, x = 1 é uma raiz desse polinômio. Para achar as outras, precisamos aplicar um processo de redução de grau. Tipicamente, esse processo é realizado aplicando-se o dispositivo prático de Briot-Ruffini. Após a aplicação desse processo, você deve obter:
. Ou seja, x = 1 é uma raiz desse polinômio. Para achar as outras, precisamos aplicar um processo de redução de grau. Tipicamente, esse processo é realizado aplicando-se o dispositivo prático de Briot-Ruffini. Após a aplicação desse processo, você deve obter: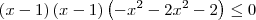


 .
.
 :
: