 por elisamaria » Qui Jun 11, 2015 16:56
por elisamaria » Qui Jun 11, 2015 16:56
Considere z um número complexo cujas partes, real e imaginária, não se anulam simultaneamente. Então, os números complexos que satisfazem a equação z + 1/z = 1, possuem módulo igual a:
a) 1/2.
b) ?3/2.
c) ?3.
d) 1.
-
elisamaria
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 09, 2015 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Qui Jun 11, 2015 19:20
por nakagumahissao » Qui Jun 11, 2015 19:20
Resolução:
[1]
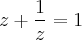
Tomemos z como sendo:
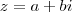
e substituindo em [1], teremos:
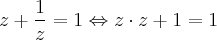
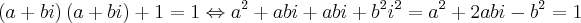
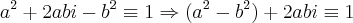
Desta última sabemos o valor Real e o imaginário necessário para calcular a e b. Dessa maneira, temos que:
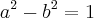
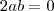
Desta última, sabemos que a ou b vale 0, mas não ambos, pois as partes, real e imaginária, não se anulam simultaneamente conforme o enunciado.
Façamos b = 0 e calculemos a:

Portanto, a e b poderão ser:
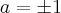

ou
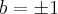

Quanto ao módulo sendo procurado, para quaisquer um dos resultados acima, deverá ser:
![\left|z \right| = \sqrt[]{\left(\pm 1 \right)^{2} + 0^2} = 1 \left|z \right| = \sqrt[]{\left(\pm 1 \right)^{2} + 0^2} = 1](/latexrender/pictures/cb7a8e65254e8518c579c8c1f4c60751.png)
Portanto, a opção correta é a letra (D).
Espero ter auxiliado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números Complexos] Módulo.
por HCF01 » Dom Fev 02, 2014 15:21
- 2 Respostas
- 5291 Exibições
- Última mensagem por e8group

Seg Fev 03, 2014 19:57
Números Complexos
-
- duvidas dois numeros irracionais
por hevhoram » Qui Jun 24, 2010 11:56
- 2 Respostas
- 2484 Exibições
- Última mensagem por MarceloFantini

Qui Jun 24, 2010 14:03
Álgebra Elementar
-
- Razão entre dois números
por lucas7 » Qui Fev 24, 2011 21:21
- 1 Respostas
- 2086 Exibições
- Última mensagem por lucas7

Sex Fev 25, 2011 08:44
Sistemas de Equações
-
- Maior entre dois numeros
por TiagoRodrigues » Qui Mar 01, 2012 14:37
- 5 Respostas
- 3932 Exibições
- Última mensagem por TiagoRodrigues

Sex Mar 02, 2012 11:18
Sistemas de Equações
-
- Demonstração de igualdade de dois números ao quadrado
por johnlaw » Sáb Mar 05, 2011 18:15
- 9 Respostas
- 5406 Exibições
- Última mensagem por johnlaw

Sex Mar 11, 2011 01:43
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



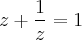
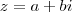
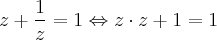
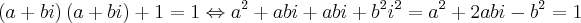
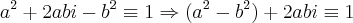
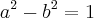
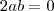

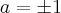

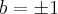

![\left|z \right| = \sqrt[]{\left(\pm 1 \right)^{2} + 0^2} = 1 \left|z \right| = \sqrt[]{\left(\pm 1 \right)^{2} + 0^2} = 1](/latexrender/pictures/cb7a8e65254e8518c579c8c1f4c60751.png)
