 por Vennom » Sáb Jul 21, 2012 06:57
por Vennom » Sáb Jul 21, 2012 06:57
Senhores, bom dia. Nessa semana que se passou eu iniciei meus estudos de números complexos e, mediante o exercício em que lhes peço ajuda a seguir eu travei. Sequer consegui desenvolver um esboço de resolução. Se alguém aqui puder gentilmente me 'dar uma luz':
Fundamentos da Matemática Elementar, vol 6, exercício 16, pag 11:
Quais os números complexos x e y para os quais : x + yi = i e xi + y = 2i - 1 .
Seguindo o raciocínio que eu aprendi a ter até agora pelas coisas ditas pelo livro eu consideraria isso daí duas funções separadas e diria que para a primeira, considerando que real é igual a real e imaginário é igual a imaginário, diria que:
x = 0 e y = 1 ; na segunda eu diria que : x = 2 e y = -1 entretanto o gabarito é único e me apresenta a seguinte resposta:
x = 1 + i ; y = i
Logo em seguida vem o exercício 18, na pag 12:
Qual a condição para que o número
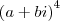
, a e b reais, seja estritamente negativo?
Nesse aí eu parti do seguinte princípio:

, então eu cheguei a algo como
![{(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2} {(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2}](/latexrender/pictures/dfdefc57b1a35b851ae34a31f5224b3e.png)
; então:
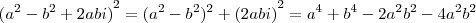
, sendo essa última menor que zero, pois a condição do enunciado é que sejam menores que zero, então:
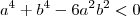
; disso eu consigo dizer somente que ab tem que ser diferentes de zero;
já na resposta do livro o gabarito também chega a conclusão de que a = +-b ; essa última parte eu não sei como ele alcançou ou se minhas ponderações até aqui também foram corretas.
Obrigado a quem ler e se interessar a responder. Att, Rafael.
Editado pela última vez por
Vennom em Sáb Jul 21, 2012 07:23, em um total de 1 vez.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sáb Jul 21, 2012 07:21
por Russman » Sáb Jul 21, 2012 07:21
Vennom:
A relação
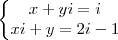
é um sistema linear de 2 incógnitas,

e

, de 2 equações. Portanto o par
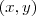
da 1° equação é identico ao par
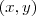
da segunda equação.
A sua estimativa não estaria errada se considerássemos equações independentes. Mas não são.
A solução deste sistema segue como a de um sistema linear a variáveis reais.
Eu costumo resolver da seguinte forma: isole uma das incógnitas em uma equação e aplique na outra. Calculada essa incógnita, calcule a outra usando o valor desta.
Então, isolando

na 1° equação vem
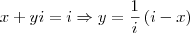
.
Aplicando na 2° equação, temos
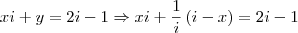
,
e, portanto,

.
Agora, com este resultado, calculamos

.
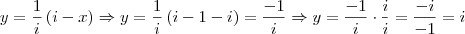
.
Assim, a solução do sistema linear é
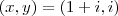
.
Alguma dúvida?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Vennom » Sáb Jul 21, 2012 07:26
por Vennom » Sáb Jul 21, 2012 07:26
Até agora com relação a primeira pergunta, sua explicação foi maravilhosamente perfeita. Tem como me ajudar sobre minha edição aí na pergunta com relação a segunda dúvida?
Ps.: obrigado Russman.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Vennom » Sáb Jul 21, 2012 07:29
por Vennom » Sáb Jul 21, 2012 07:29
Para complementar, nessa parte aqui na parte do y = -1/i , você multiplica por i/i por que? Eu não posso ter a unidade imaginária no denominador e por isso tenho que aplicar a regra da racionalização?
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sáb Jul 21, 2012 08:09
por Russman » Sáb Jul 21, 2012 08:09
É convencional que expressemos sempre um número complexo na forma

. Portanto, a solução
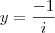
é correta porém, de certa forma, inadequada. Para resolver este problema basta que você multiplique o denominador e numerador pelo conjugado do número complexo que aparece no denominador.
Note que
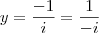
.
O conjugado do complexo

é

. Portanto, segue o processo. Apenas uma observação: esta regra não é a da racionalização, visto que nesta o interesse é em escrever o denominador como um número racional( daí, racionalizar). Nosso objetivo é tornar o denominador real.
De forma geral, se você se deparar com o problema de expressar na forma convencional, isto é,

, o complexo, por exemplo,
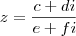
basta que o multiplique pelo conjugado do denominador, isto é, por

, visto que o produto de um numero complexo por seu conjugado é sempre um número real puro!
Segue que
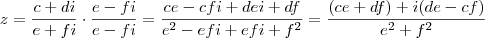
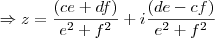
onde

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Sáb Jul 21, 2012 08:41
por Russman » Sáb Jul 21, 2012 08:41
Russman escreveu:Qual a condição para que o número , a e b reais, seja estritamente negativo?
Antes de ajudá-lo nesta questão eu gostaria de corrigí-lo.
Na parte que você escreveu
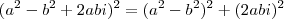
tome cuidado, pois isto não é verdade! Reveja produtos notáveis.
Voltando a questão: um número complexo não pode ser classificado quanto a positivo ou negativo. Oque podemos fazer é classificar suas pates real e imaginária pois são reais.
Assim, a primeira coisa a fazer é determinar a relação de

com

para que o complexo apresentado seja um real puro! Para tanto é necessário que sua parte imaginária seja nula. Vamos expandir o complexo para isolar sua parte real e imaginária:
![(a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi) (a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi)](/latexrender/pictures/c08937a213c7515a2376dfb8a85ff409.png)
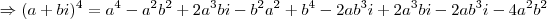
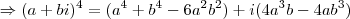
.
Veja, que a parte imaginária de
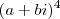
é

que deve ser nula. Portanto,
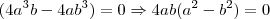
.
Desta, tiramos três soluções possíveis:

Mas ainda queremos que o número seja negativo, isto é, a parte real do número seja negativa ( uma vez qe ele será real puro pois tomamos a parte imaginária nula). Assim, teremos de testar as 3 soluções obtidas anteriormente na parte real e verificar se ela será negativa!
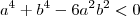
Se tomarmos a 1° solução

, então
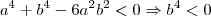
,
o que é um absurdo, visto que qualquer real elevado a uma potência par é sempre positivo. Assim, esta não é válida. Descartamos a solução

.
Para

acontecerá o mesmo!
Para

, temos
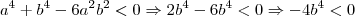
.
Isto é verdade para todo b real, pois o produto de um negativo com um positivo é sempre negativo.
O mesmo acontecerá para o caso

.
Assim, segue o resultado do gabarito.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Vennom » Sáb Jul 21, 2012 09:18
por Vennom » Sáb Jul 21, 2012 09:18
Entendido! Obrigado, Russman!
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Vennom » Seg Set 10, 2012 14:50
por Vennom » Seg Set 10, 2012 14:50
Complementando um tópico antigo meu, mais duas perguntas sobre o mesmo assunto...
Livro: Fundamentos da Matemática Elementar, vol 6, pg. 44, exercício 84, alternativas C e D.
![\sqrt[3]{-11-2i} \sqrt[3]{-11-2i}](/latexrender/pictures/dd0627ec5e478d7b61a8f7c4a7c05ce9.png)
![\sqrt[4]{28-96i} \sqrt[4]{28-96i}](/latexrender/pictures/5cf4fdfd1c7fa2b54dd0ce17967ccdc0.png)
Os respectivos gabaritos são :
1°) 1+2i ou
![\frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/24a072a19043a10ec7c3ea59e63c2d03.png)
ou
![\frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/078ff3bde8a90ebdae5d5e838be5db33.png)
2°) -3+i ou 3-i ou 1+3i ou -1-3i
Eu tentei aplicar a segunda fórmula de Moivre, mas me perco nesses dois últimos, só consegui com raízes quadradas.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Set 10, 2012 15:56
por Russman » Seg Set 10, 2012 15:56
A fórmula de Moivre calcula potências e as

raízes

-ésimas de um número, em geral, complexo! Mas veja que a mesma calcula raízes de números puramente reais também( claro, todo Real é complexo).
Seja

um complexo de argumento

. Assim,
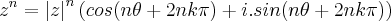
onde
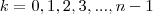
.
No primeiro caso, temos
![\sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right) \sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right)](/latexrender/pictures/93e38e6ef757d2d70369fd696547c5fa.png)
onde

.
Agora faça
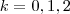
e calcule as 3 raízes.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz número complexo] Exercício fora do padrão
por Bruno G Carneiro » Sex Jun 08, 2012 20:54
- 1 Respostas
- 2099 Exibições
- Última mensagem por fraol

Qua Jun 20, 2012 22:35
Números Complexos
-
- [módulo do número complexo]
por JKS » Qui Jun 20, 2013 01:56
- 1 Respostas
- 3055 Exibições
- Última mensagem por MateusL

Qui Jul 18, 2013 19:49
Números Complexos
-
- Equação de número complexo
 por YuriFreire » Seg Set 01, 2014 21:44
por YuriFreire » Seg Set 01, 2014 21:44
- 3 Respostas
- 5141 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 21:19
Números Complexos
-
- somatória com número complexo
por ezidia51 » Qua Abr 04, 2018 17:44
- 3 Respostas
- 10528 Exibições
- Última mensagem por Gebe

Qui Abr 05, 2018 13:32
Números Complexos
-
- Numero Complexo, resistência e reatância
por Fran Ianhez » Ter Set 27, 2016 23:07
- 0 Respostas
- 6230 Exibições
- Última mensagem por Fran Ianhez

Ter Set 27, 2016 23:07
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
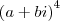 , a e b reais, seja estritamente negativo?
, a e b reais, seja estritamente negativo? , então eu cheguei a algo como
, então eu cheguei a algo como ![{(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2} {(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2}](/latexrender/pictures/dfdefc57b1a35b851ae34a31f5224b3e.png) ; então:
; então: 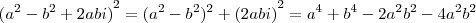 , sendo essa última menor que zero, pois a condição do enunciado é que sejam menores que zero, então:
, sendo essa última menor que zero, pois a condição do enunciado é que sejam menores que zero, então: 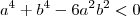 ; disso eu consigo dizer somente que ab tem que ser diferentes de zero;
; disso eu consigo dizer somente que ab tem que ser diferentes de zero; 

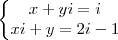
 e
e  , de 2 equações. Portanto o par
, de 2 equações. Portanto o par 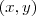 da 1° equação é identico ao par
da 1° equação é identico ao par 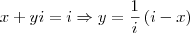 .
.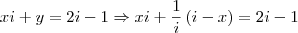 ,
, .
.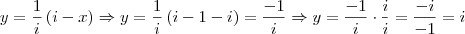 .
.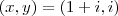 .
.
 . Portanto, a solução
. Portanto, a solução 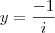 é correta porém, de certa forma, inadequada. Para resolver este problema basta que você multiplique o denominador e numerador pelo conjugado do número complexo que aparece no denominador.
é correta porém, de certa forma, inadequada. Para resolver este problema basta que você multiplique o denominador e numerador pelo conjugado do número complexo que aparece no denominador.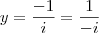 .
. é
é  . Portanto, segue o processo. Apenas uma observação: esta regra não é a da racionalização, visto que nesta o interesse é em escrever o denominador como um número racional( daí, racionalizar). Nosso objetivo é tornar o denominador real.
. Portanto, segue o processo. Apenas uma observação: esta regra não é a da racionalização, visto que nesta o interesse é em escrever o denominador como um número racional( daí, racionalizar). Nosso objetivo é tornar o denominador real.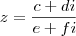
 , visto que o produto de um numero complexo por seu conjugado é sempre um número real puro!
, visto que o produto de um numero complexo por seu conjugado é sempre um número real puro!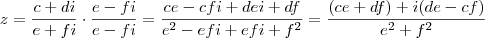
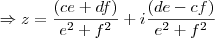
 .
.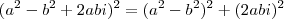
 com
com  para que o complexo apresentado seja um real puro! Para tanto é necessário que sua parte imaginária seja nula. Vamos expandir o complexo para isolar sua parte real e imaginária:
para que o complexo apresentado seja um real puro! Para tanto é necessário que sua parte imaginária seja nula. Vamos expandir o complexo para isolar sua parte real e imaginária:![(a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi) (a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi)](/latexrender/pictures/c08937a213c7515a2376dfb8a85ff409.png)
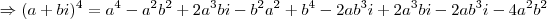
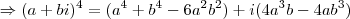 .
.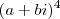 é
é  que deve ser nula. Portanto,
que deve ser nula. Portanto,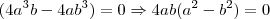 .
.
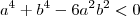
 , então
, então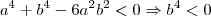 ,
, acontecerá o mesmo!
acontecerá o mesmo! , temos
, temos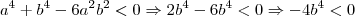 .
. .
.![\sqrt[3]{-11-2i} \sqrt[3]{-11-2i}](/latexrender/pictures/dd0627ec5e478d7b61a8f7c4a7c05ce9.png)
![\sqrt[4]{28-96i} \sqrt[4]{28-96i}](/latexrender/pictures/5cf4fdfd1c7fa2b54dd0ce17967ccdc0.png)
![\frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/24a072a19043a10ec7c3ea59e63c2d03.png) ou
ou ![\frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/078ff3bde8a90ebdae5d5e838be5db33.png)
 raízes
raízes  um complexo de argumento
um complexo de argumento  . Assim,
. Assim,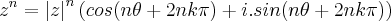
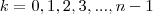 .
.![\sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right) \sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right)](/latexrender/pictures/93e38e6ef757d2d70369fd696547c5fa.png)
 .
.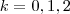 e calcule as 3 raízes.
e calcule as 3 raízes.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
