 por Fabricio dalla » Sex Abr 01, 2011 01:13
por Fabricio dalla » Sex Abr 01, 2011 01:13
(ITA)Determine o termo independente de x no desenvolvimento do binomio :
![({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12} ({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12}](/latexrender/pictures/fada54dc420f83d9a108cfe0679b647a.png)
olha eu perguntei pro meu professor ele falou q tinha q resolve os radicais dentro do binomio. bom entao o que entendi dele seria resolver essa moleza :( ate onde der para poder identificar os o coeficiente a e o X" para jogar na formula. o problema racionalizaçao so serve pra indice 2 que eu me lembre.Então acredito que se deve chegar de outro modo aos coeficientes. se possivel me oriente o que devo fazer!!.
obs(será que o coeficiente de X" ai seria o x de maior expoente no caso x elevado a 2/3 ?)
resposta:
![165\sqrt[3]{75} 165\sqrt[3]{75}](/latexrender/pictures/6becbc7c377927576ddabf23d26ae909.png)
desde ja agradeço
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Abr 01, 2011 12:04
por LuizAquino » Sex Abr 01, 2011 12:04
Ao invés de "lhe dar o peixe", eu vou "lhe ensinar a pescar".
Com uma rápida pesquisa no
Google, achei que essa prova foi do vestibular 2004 do ITA. Nessa mesma pesquisa, achei a questão resolvida:
http://www.elitecampinas.com.br/gabaritos/ita/ita_04_mat_ELITE.pdfAproveito então para deixar essa dica.
Antes de enviar uma dúvida para o Fórum, não custa dar uma procurada pela internet. Ou até mesmo, usar o botão de busca daqui do Fórum. Eu já vi diversas questões repetidas aqui. Isso não aconteceria se a pessoa primeiro procurasse pela questão antes de enviá-la.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Sex Abr 01, 2011 15:37
por Fabricio dalla » Sex Abr 01, 2011 15:37
pow vlws entendi tudo, so que tenho uma duvida exemplo:
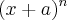
sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento
dentro do parenteses do binomio ou vc tem que identificar primeiro qual a variavel dentro do parenteses do binomio de maior expoente e falar que é "X" para usar a formula ?
vou seguir o seu conselho de antes de perguntar pesquisar a resoluçao do exercicio
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Abr 01, 2011 16:34
por LuizAquino » Sex Abr 01, 2011 16:34
Fabricio dalla escreveu: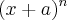
sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento
dentro do parenteses do binomio ou vc tem que identificar primeiro qual a variavel dentro do parenteses do binomio de maior expoente e falar que é "X" para usar a formula ?
Isso não importa. As duas operações abaixo resultam no mesmo polinômio:
(i)
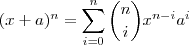
(ii)
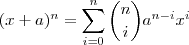
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Sex Abr 01, 2011 23:47
por Fabricio dalla » Sex Abr 01, 2011 23:47
e msm tanto faz piff!obrigado pela atenção mais uma vez
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por bia lima » Sáb Jul 23, 2011 17:18
por bia lima » Sáb Jul 23, 2011 17:18
preciso de ajuda! estou no inicio do assunto de binomio de newton e ainda nao consegui enteder e estou sem enteder a questao:
"o coeficiente do termo independente de x, no desenvolvimento do binômio (2x

, é:
a- 15
b-30
c- 60
d- 120
e- 240
obrigada pela atenção e ajuda.
-
bia lima
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jul 23, 2011 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Jul 23, 2011 17:39
por LuizAquino » Sáb Jul 23, 2011 17:39
Olá bia lima,
Por questão de organização, cada tópico deve ter apenas um exercício.
Desse modo, por favor crie um novo tópico com a sua dúvida.
Além disso, no novo tópico procure escrever a expressão mais organizada. Por acaso não seria
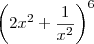
?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por bia lima » Sáb Jul 23, 2011 19:02
por bia lima » Sáb Jul 23, 2011 19:02
nossa, é isso mesmo. muito obrigada. estou meio atrapalhada ainda no assunto e em como usar o site. bom, se voce puder me ajudar... agradecerei muito.
-
bia lima
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jul 23, 2011 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Jul 23, 2011 19:12
por LuizAquino » Sáb Jul 23, 2011 19:12
bia lima escreveu:nossa, é isso mesmo. muito obrigada. estou meio atrapalhada ainda no assunto e em como usar o site.
Para criar um novo tópico siga os passos:
1) Escolha a seção onde vai postar a sua dúvida. Nessa caso, a seção é
Binômio de Newton;
2) Clique no botão "Novo tópico" (como ilustra a figura abaixo) para acrescentar o seu tópico;
- novo-tópico.png (28.46 KiB) Exibido 8213 vezes
3) Pronto. Uma nova página irá abrir e nela você poderá digitar o seu tópico. Após finalizar, basta clicar no botão "Enviar".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8109 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 7391 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8817 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
-
- Binomio de Newton.
por 380625 » Sex Mar 11, 2011 12:57
- 1 Respostas
- 3024 Exibições
- Última mensagem por MarceloFantini

Sex Mar 11, 2011 16:20
Binômio de Newton
-
- BINOMIO DE nEWTON
por clabonfim » Qua Jan 11, 2012 12:50
- 2 Respostas
- 3553 Exibições
- Última mensagem por clabonfim

Qui Jan 26, 2012 02:05
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12} ({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12}](/latexrender/pictures/fada54dc420f83d9a108cfe0679b647a.png)
![165\sqrt[3]{75} 165\sqrt[3]{75}](/latexrender/pictures/6becbc7c377927576ddabf23d26ae909.png)



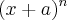 sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento
sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento 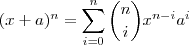
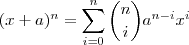
 , é:
, é:
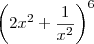 ?
?
 .
.
 :
: