 por natanskt » Qua Dez 01, 2010 13:37
por natanskt » Qua Dez 01, 2010 13:37
calcule o valor de n nas sentenças
a-)

nessa questão eu achei como resposta 41/5,só que fala que é 7
b-)

achei como resposta

,porém o exercicio fala que é 8.
se eu estiver certo,por favor alguem pode acabar essa conta pq eu ainda não sei fazer quando tem n^3
agora esse pede para simpificar a expressão:
c-)

nessa a mesma coisa
cheguei a

o exercicio fala que é 1/n+2
desculpa galera se coloquei 3 questões é que são faceis demais,nem haveria necessidade de criar outro tópico com questões desse nivel.
eu que sou lerdo mesmo.
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por alexandre32100 » Qua Dez 01, 2010 15:29
por alexandre32100 » Qua Dez 01, 2010 15:29
a.
Não sei se a resposta é
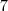
, por que

(pode verificar!)
Também tentei algo do tipo


(pode dividir toda expressão por

)

(aqui também dá pra simplificar tudo por
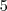
)

E não cheguei a
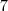
.
b.


Nessa, realmente,

.
c.

-
alexandre32100
-
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatorial
por elisonsevalho » Sex Mar 05, 2010 17:22
- 3 Respostas
- 2415 Exibições
- Última mensagem por Molina

Sáb Mar 06, 2010 14:49
Álgebra Elementar
-
- Fatorial.
por vanessasuellen » Qua Set 07, 2011 21:37
- 1 Respostas
- 1722 Exibições
- Última mensagem por Aliocha Karamazov

Sex Set 09, 2011 01:36
Estatística
-
- Fatorial de 0
por Neperiano » Qua Set 14, 2011 19:45
- 16 Respostas
- 9581 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 15:48
Estatística
-
- fatorial
por andersontricordiano » Sáb Fev 11, 2012 13:44
- 1 Respostas
- 1422 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 14:50
Estatística
-
- fatorial
por andersontricordiano » Sáb Fev 11, 2012 20:31
- 1 Respostas
- 1369 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 20:43
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ,porém o exercicio fala que é 8.
,porém o exercicio fala que é 8.



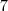 , por que
, por que (pode verificar!)
(pode verificar!)
 (pode dividir toda expressão por
(pode dividir toda expressão por  )
) (aqui também dá pra simplificar tudo por
(aqui também dá pra simplificar tudo por 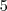 )
)


 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.