No calculo de (x²+xy)^15, o termo em que o grau de x é 21 vale:
Ps: a resposta é 5005x^21y^9, preciso de ajuda com a resolução
Att, Jhenny ;*



![(x^2 + xy)^{15} = (x[x+y])^{15} = x^{15}[x+y]^15 (x^2 + xy)^{15} = (x[x+y])^{15} = x^{15}[x+y]^15](/latexrender/pictures/0dd56839cfcbbead5db39445b8c5d9a6.png) .O termo em que o grau de
.O termo em que o grau de  é grau 21 será o termo que contém "x de grau 6" de
é grau 21 será o termo que contém "x de grau 6" de ![[x+y]^{15} [x+y]^{15}](/latexrender/pictures/526c1126e769359a1f144cf8bce6dddb.png) .Logo pelo binômio de newton ,tiramos que o termo que possui x com grau 6 é
.Logo pelo binômio de newton ,tiramos que o termo que possui x com grau 6 é 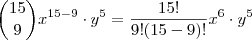 .Multiplicando por
.Multiplicando por 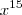 resulta
resulta 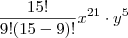 .
. ![(x^2 + xy)^15 = (x[x+y])^15 = x^15[x+y]^15 (x^2 + xy)^15 = (x[x+y])^15 = x^15[x+y]^15](/latexrender/pictures/00595a4623dfae87707506c7f0b4d13a.png) .Cada termo ou parcela do desenvolvimento
.Cada termo ou parcela do desenvolvimento 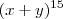 pelo binômio de newton pode ser escrito por
pelo binômio de newton pode ser escrito por 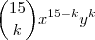 para
para 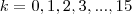 .Assim , se
.Assim , se  é o primeiro termo ,
é o primeiro termo ,  segundo termo e assim sucessivamente . Aplicando a distributiva de
segundo termo e assim sucessivamente . Aplicando a distributiva de 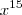 sobre
sobre 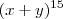 expandido pelo binômio de newton ,cada parcela(ou termo ) será multiplicada(o) por
expandido pelo binômio de newton ,cada parcela(ou termo ) será multiplicada(o) por 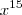 , então o mesmo será dado por
, então o mesmo será dado por 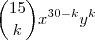 . Fazendo
. Fazendo 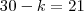 obtemos
obtemos  . Segue então o resultado ..
. Segue então o resultado ..

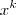 (k natural) ,o termo
(k natural) ,o termo  possui grau k .Se queremos encontar o termo que o grau de x é 21 .Como ja temos
possui grau k .Se queremos encontar o termo que o grau de x é 21 .Como ja temos 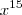 (o grau de x é 15) multiplicando
(o grau de x é 15) multiplicando 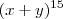 , a conclusão é que precisamos encontrar um termo de
, a conclusão é que precisamos encontrar um termo de 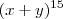 em que o grau de
em que o grau de  é 6 . Pois
é 6 . Pois 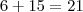 , lembre-se em produto de potências de mesma base conserva a base e soma os expoentes . Assim, por exemplo :
, lembre-se em produto de potências de mesma base conserva a base e soma os expoentes . Assim, por exemplo : 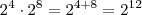 .Em resumo ao desenvolver
.Em resumo ao desenvolver 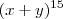 pelo binômio de newton precisamos encontar um termo que contém x de grau 6 ,isto é,
pelo binômio de newton precisamos encontar um termo que contém x de grau 6 ,isto é, 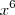 (não importa o grau de y) por que
(não importa o grau de y) por que 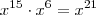 .Segue então que o termo que contém x com o grau 6 é
.Segue então que o termo que contém x com o grau 6 é 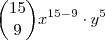 conforme eu já postei acima , inclusive uma solução alternativa .
conforme eu já postei acima , inclusive uma solução alternativa . 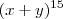 no seguinte link :
no seguinte link : 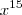 multiplicando
multiplicando 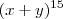 temos então que em todas parcelas que contém a base
temos então que em todas parcelas que contém a base  , o grau de
, o grau de  aumentará em 15 , estamos somando
aumentará em 15 , estamos somando  no expoente da base
no expoente da base  .
. 

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

