 por silvia fillet » Seg Abr 30, 2012 13:49
por silvia fillet » Seg Abr 30, 2012 13:49
Utilizando um argumento combinatorio mostre que


fixe um elemento do conjunto e conte o total de subconjuntos de tamanho k que contem o elemento e o total de subconjuntos de tamnho k que nao o contem.
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Aparecida » Sáb Mai 05, 2012 00:06
por Aparecida » Sáb Mai 05, 2012 00:06
1. Um lote contém 12 itens bons e 8 itens defeituosos. Uma amostra de 5 itens é extraída. Determine o total de amostras contendo exatamente 3 itens bons.
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por Fabiano Vieira » Sáb Mai 05, 2012 11:59
por Fabiano Vieira » Sáb Mai 05, 2012 11:59
Aparecida escreveu:1. Um lote contém 12 itens bons e 8 itens defeituosos. Uma amostra de 5 itens é extraída. Determine o total de amostras contendo exatamente 3 itens bons.
Aparecida,
para melhor organização do fórum, quando for postar uma questão abra um novo tópico.
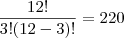
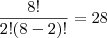

-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por psdias » Sáb Mai 05, 2012 22:00
por psdias » Sáb Mai 05, 2012 22:00
Olá, Fabiano !
Fiz as mesmas contas que você, chegando a 220 e 28, mas
eu MULTIPLIQUEI esses valores, chegando a 6.160.
Não entendi porque você somou os dois resultados. Pode explicar, por favor ?
Obs.: No seguinte link, há um problema semelhante, apenas mudando a quantidade de peças boas e defeituosas, e o tamanho da amostra:
http://www.ebah.com.br/content/ABAAABql ... mbinatoriaPaulo
-
psdias
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Nov 22, 2011 18:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: LICENCIATURA EM MATEMÁTICA
- Andamento: formado
 por Fabiano Vieira » Dom Mai 06, 2012 01:21
por Fabiano Vieira » Dom Mai 06, 2012 01:21
psdias escreveu:Olá, Fabiano !
Fiz as mesmas contas que você, chegando a 220 e 28, mas
eu MULTIPLIQUEI esses valores, chegando a 6.160.
Não entendi porque você somou os dois resultados. Pode explicar, por favor ?
Olhei o exercício do link, é igual. Foi um erro meu nessa questão.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- analise combinatoria probabilidade
por silvia fillet » Sex Abr 27, 2012 19:55
- 4 Respostas
- 4567 Exibições
- Última mensagem por Tiego

Qua Mai 09, 2012 10:17
Estatística
-
- analise combinatoria probabilidade
por silvia fillet » Sex Mai 11, 2012 20:45
- 6 Respostas
- 5674 Exibições
- Última mensagem por debeta56

Sáb Mai 12, 2012 17:12
Estatística
-
- Analise combinatória e probabilidade
por Lucianon » Ter Mai 06, 2014 21:39
- 0 Respostas
- 2770 Exibições
- Última mensagem por Lucianon

Ter Mai 06, 2014 21:39
Estatística
-
- Analise combinatória e probabilidade
por Lucianon » Ter Mai 06, 2014 21:40
- 0 Respostas
- 2342 Exibições
- Última mensagem por Lucianon

Ter Mai 06, 2014 21:40
Análise Combinatória
-
- analise combinatoria probabilidade estatistica
por silvia fillet » Sex Mai 11, 2012 20:41
- 1 Respostas
- 4517 Exibições
- Última mensagem por leomjr

Qui Mai 17, 2012 17:22
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







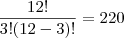
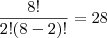






 , avisa que eu resolvo.
, avisa que eu resolvo.

