 por LuizCarlos » Ter Abr 24, 2012 20:04
por LuizCarlos » Ter Abr 24, 2012 20:04
Olá amigos, professores, boa noite!
Estou tentando resolver uns exercícios de Medidas Estatísticas, mas essa questão, resolvi, porém não tenho certeza se está correta!
Num feriado prolongado desceram para as praias do litoral paulista
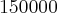
carros. Se 10 por cento tinham só o motorista, 20 por cento tinham duas pessoas, 20 por cento tinham três pessoas, 30 por cento tinham quatro pessoas, e 20 por cento tinham cinco pessoas, em média, quantas pessoas havia por carro.
Tentei resolver dessa forma:
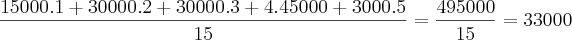
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Ter Abr 24, 2012 20:40
por DanielFerreira » Ter Abr 24, 2012 20:40
Pelo que entendi seria:
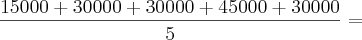
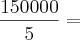
30.000
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Ter Abr 24, 2012 22:35
por LuizCarlos » Ter Abr 24, 2012 22:35
danjr5 escreveu:Pelo que entendi seria:
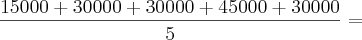
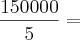
30.000
Olá amigo danjr5, boa noite! creio que você não conseguiu entender o que escrevi, pelo fato de não estar aparecendo corretamente o problema no seu computador! a resposta no livro é 3,3 pessoas.
Mas creio que isso deve ser resolvido com uma média ponderada, você fez uma média aritmética!
Não consigo escrever os exercícios legível pelo fato do meu teclado ser em outra língua, uso um notebook que ganhei de presente, mas estarei comprando um teclado, para digitar os exercícios para que apareçam legivelmente.
O problema é o seguinte:
Num feriado prolongado, desceram para as praias do litoral paulista

carros. Se

por cento dos carros tinham apenas o motorista,
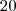
por cento tinham

pessoas,
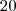
por cento tinham

pessoas,
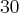
por cento tinham

pessoas e
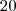
por cento tinham cinco pessoas, em média, quantas pessoas havia por carro.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Qua Abr 25, 2012 18:05
por LuizCarlos » Qua Abr 25, 2012 18:05
Consegui resolver a questão, obrigado pela ajuda!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em Questão de (EDO)
por sys_ » Sex Abr 10, 2009 19:06
- 2 Respostas
- 2329 Exibições
- Última mensagem por nakagumahissao

Seg Ago 17, 2015 13:04
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:18
- 3 Respostas
- 7270 Exibições
- Última mensagem por DanielFerreira

Dom Ago 23, 2009 12:59
Progressões
-
- Dúvida na questão
por GABRIELA » Ter Set 01, 2009 17:17
- 2 Respostas
- 6171 Exibições
- Última mensagem por Molina

Ter Set 01, 2009 23:28
Matrizes e Determinantes
-
- duvida na questão
por GABRIELA » Qua Set 30, 2009 17:06
- 10 Respostas
- 6692 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 22:42
Geometria Analítica
-
- Dúvida em uma questão
por Padoan » Qua Ago 11, 2010 18:53
- 3 Respostas
- 3225 Exibições
- Última mensagem por Padoan

Sex Ago 13, 2010 23:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
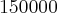 carros. Se 10 por cento tinham só o motorista, 20 por cento tinham duas pessoas, 20 por cento tinham três pessoas, 30 por cento tinham quatro pessoas, e 20 por cento tinham cinco pessoas, em média, quantas pessoas havia por carro.
carros. Se 10 por cento tinham só o motorista, 20 por cento tinham duas pessoas, 20 por cento tinham três pessoas, 30 por cento tinham quatro pessoas, e 20 por cento tinham cinco pessoas, em média, quantas pessoas havia por carro.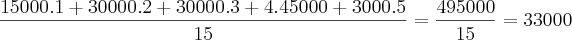


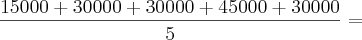
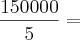

 carros. Se
carros. Se  por cento dos carros tinham apenas o motorista,
por cento dos carros tinham apenas o motorista, 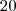 por cento tinham
por cento tinham  pessoas,
pessoas,  pessoas,
pessoas, 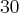 por cento tinham
por cento tinham  pessoas e
pessoas e 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.