 por DanielRJ » Qua Set 22, 2010 14:43
por DanielRJ » Qua Set 22, 2010 14:43
Considere dois eventos indenpedentes A e B de um mesmo espaço amostral.Sabendo que
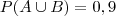
e
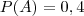
e
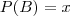
. O valor de x é?
a)1/6
b)2/3
c)5/6
d)1/3
Bom pessoal fiz uma busca com relação a questão na net e não obitive êxito, então vamos ver se vcs conseguem me ajudar. sobre a questão eu sei o seguinte:
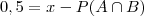 Substituindo os valores e paro na seguinte expressão e travo!
Substituindo os valores e paro na seguinte expressão e travo! 
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qua Set 22, 2010 15:11
por Molina » Qua Set 22, 2010 15:11
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10349 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21659 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5349 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4523 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4536 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
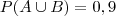 e
e 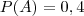 e
e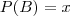 . O valor de x é?
. O valor de x é?
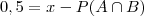 Substituindo os valores e paro na seguinte expressão e travo!
Substituindo os valores e paro na seguinte expressão e travo! 


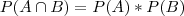
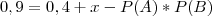


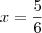

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)