Por favor me ajudem!!

[Anderson POntes]

Em uma fábrica de bijuterias são produzidos colares enfeitados
com cinco contas de mesmo tamanho dispostas lado a
lado, como mostra a figura.

colar.JPG (5.35 KiB) Exibido 2148 vezes

As contas estão disponíveis em 8 cores diferentes.
De quantos modos distintos é possível escolher as cinco
contas para compor um colar, se a primeira e a última
contas devem ser da mesma cor, a segunda e a penúltimacontas devem ser da mesma cor e duas contas consecutivas
devem ser de cores diferentes?
(A) 336 (B) 392
(C) 448 (D) 556
(E) 612

[alexandre32100]

Para isso, basta apenas definir as cores das três primeiras contas, afinal as outras duas têm suas cores definidas de acordo com as das duas primeiras.
Para a primeira conta pode-se escolher cada uma das cores, para a segunda, 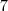(todas, menos a escolhida para a primeira conta) e para a terceira, mais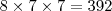 (ela pode ter a mesma cor da primeira, afinal, não são consecutivas), totalizando:
(alternativa B)

[Anderson POntes]

Muito obrigado!!