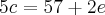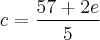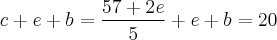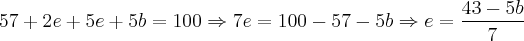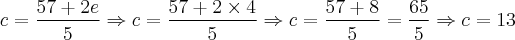Veja bem, na questão que postou, mais uma pequena informação deveria ter sido fornecida. Considerarei que esteja correta e resolveremos da seguinte forma:
Sabendo-se que 5 pontos são ganhos por cada resposta certa, perde-se 2 pontos para cada errada e se ganha 0 pontos para cada uma deixada em branco, seja c o número de respostas certas, e o número de cada resposta errada e b o número de cada resposta deixada em branco, tem-se que:
[1] 5c - 2e =57
e
[2] c + e + b = 20
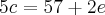
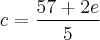
Usando esta última equação obtida em [2] acima, tem-se que:
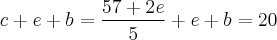
Multiplicando-se ambos os lados por cinco, teremos:
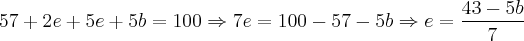
Como uma informação parece estar faltando, por tentativa e erro, tentaremos descobrir o valor de b. Veja a tabela abaixo:
Para b = 0 => e = 43/7 que não é um valor inteiro
Para b = 1 => e = 38/7 que não é um valor inteiro
Para b = 2 => e = 33/7 que não é um valor inteiro
Para b = 3 => e=28/7 = 4
Para b = 4 => e = 23/7 que não é um valor inteiro
Para b = 5 => e = 18/7 que não é um valor inteiro
Para b = 6 => e = 13/7 que não é um valor inteiro
Para b = 7 => e = 8/7 que não é um valor inteiro
Para b = 8 => e = 3/7 que não é um valor inteiro
Para b = 9 => e < 0
Para b = 10 => e < 0
e assim por diante
Então, apenas nos interessa o valor de b sendo b = 3
Tendo este valor em mente, podemos então calcular o restante dos valores necessários
Usando b = 3, já sabemos que e = 4 e assim,
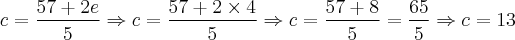
Assim, a única resposta possível para este problema seria,
13 corretas, 4 erradas e 3 deixadas em branco.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali