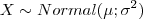. Considere o problema de estimação de 
a partir de uma amostra aleatória X1,...,Xn e considere os três estimadores abaixo: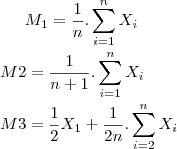
Verdadeiro ou Falso:
( ) M2 e M3 são não-eficientes.
O gabarito diz que é Verdadeiro, mas...
Comparando as 3 variâncias:
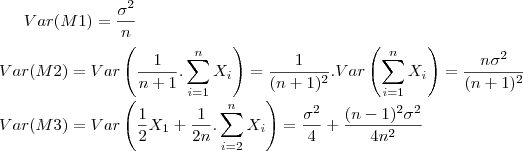
E tomando n=1,
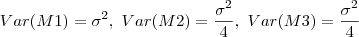
Se M2 e M3 tem variância menor, eles são eficientes relativamente a M1. Não são ???
