Preçisso de ajuda
No Brasil as placas dos veículos sao identificados por 3 letras e 4 algarismos. No estado do Paraná, que foi o primeiro do país a implatar esse sistema de emplacamentos (antes eram duas letras e quatro algarismos) , a série de placas destinadas aos veículos vai de : AAA0001 até BEZ9999
Sabendo que não existe placa com série 0000 de algarismos, calcule :
a) Quantas emplacamentos podem ser realizados no PR pelo sistema atual
Minhha resposta
Série inicial Série Final
AAA0001 BEZ9999
De A até B 2 possibilidades
De A até E 5 possibilidades
De A até Z 26possibilidades 2x5x26x10x10x10x9 = 2.340.000 possibilidaes de emplacamentos no PR
De 0 a 9 10 possibilidades
// // // 10 possibilidades está correto o que fiz ?
// // // 10 possibilidades
De 1 a 9 9 possibilidades
b) Qual a porcentagem de placas destinadas ao PR com relaçao ao total possível ?
Minha Resposta
total de emplacamentos q podem ser realizados no brasil= 26x26x26x10x10x10x10: 175.760.000
o resto não consegui resolver
c)Quantos emplacamentos podiam ser feitos no antigo sistema ? No brasil
Minha resposta
26x26x10x10x10x10 = 6.760.000
26= letras do alfabeto
10=algarismos
d) Pesquise qual é o tamanho oficial da frota nacional e responda : Quantas placas do sistema atual já foram utilizados? (resposta em % )
Minha resposta
Pesquisa : http://64.233.163.132/search?q=cache:p_ ... =firefox-a
No caso seria 51.186.302 o tamanho da frota nacional
Total de possibilidades de emplacamentos no brasil é : 175.760.000 - 51.186.302= 33.610.302
agora como trasformar esse número em porcentagem ?
Aguardando


 , pois estamos levando em consideração que a placa 0000 não exista.
, pois estamos levando em consideração que a placa 0000 não exista.
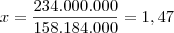



 .
.



