 por edvanio1 » Ter Nov 30, 2010 03:19
por edvanio1 » Ter Nov 30, 2010 03:19


Galera preciso que me ajudem a resolver esse exercício:
1. Considere o espaço amostral do lançamento de um dado e a observação da face superior.
Descreva, por seus elementos, os seguintes eventos:
a) A: sair face par; b) B: sair face primo;
c) C: sair face maior que 3; d) D: sair face maior que 6;
e) E: sair face múltipla de 3; f) F: sair face menor ou igual a 4;
2. O experimento consiste em lançar dois dados e observar a soma dos pontos das faces superiores. Determine o espaço amostral.
3. O experimento consiste em lançar dois dados e observar a diferença dos pontos das faces superiores. Determine o espaço amostral do experimento.
4. O experimento consiste em lançar dois dados e observar o produto dos pontos das faces superiores. Determine o espaço amostral do experimento.
5. O experimento consiste em lançar dois dados e observar em módulo, a diferença dos pontos das faces superiores. Determine o espaço amostral do experimento.
6. O experimento consiste em lançar três moedas e observar a diferença entre o número de caras e o número de coroas obtidos neste lançamento.
7. O experimento consiste em retirar duas cartas de um baralho comum e anotar ordenadamente os naipes destas cartas. Determine o espaço amostral do experimento.
-
edvanio1
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 30, 2010 03:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por alexandre32100 » Ter Nov 30, 2010 16:49
por alexandre32100 » Ter Nov 30, 2010 16:49
edvanio1 escreveu:Galera preciso que me ajudem a resolver esse exercício:
Ou seria este
s exercício
s?
Como são bastantes, acho meio chato ficar explicando um por um, mas vou tentar dar uma mão no que eu puder.
Na 1 o espaço amostral é 6 (cada face), daí, em cada item você conta as possibilidades (p) e faz
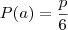
.
2. O menor caso é
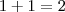
e o maior
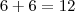
, dentre estes temos todas as possibilidades.
As questões 3, 4, 5 e 6 são bem semelhantes a 2. Basta ver a menor e maior possibilidade, as outras são todas entre estas duas.
7. Use o princípio da contagem.
-
alexandre32100
-
 por edvanio1 » Ter Nov 30, 2010 18:35
por edvanio1 » Ter Nov 30, 2010 18:35
alexandre32100 escreveu:edvanio1 escreveu:Galera preciso que me ajudem a resolver esse exercício:
Ou seria este
s exercício
s?
Como são bastantes, acho meio chato ficar explicando um por um, mas vou tentar dar uma mão no que eu puder.
Na 1 o espaço amostral é 6 (cada face), daí, em cada item você conta as possibilidades (p) e faz
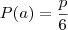
.
2. O menor caso é
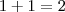
e o maior
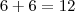
, dentre estes temos todas as possibilidades.
As questões 3, 4, 5 e 6 são bem semelhantes a 2. Basta ver a menor e maior possibilidade, as outras são todas entre estas duas.
7. Use o princípio da contagem.
Cara realmente preciso dele resolvido com urgencia, msm com as dicas nao domino o assunto, sou pessimo em calculos, se puder resolver pra mim agradeço ... vlw
-
edvanio1
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 30, 2010 03:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por alexandre32100 » Ter Nov 30, 2010 21:10
por alexandre32100 » Ter Nov 30, 2010 21:10
Amigo, como já foi discutido em outro tópico, este site não é um lugar onde você vai por as questões e elas vão sair resolvidas.
Se tiver alguma dúvida, posta aí.
Simplesmente por suas questões e achar que vai vir alguém resolvê-las é muito fácil, tente fazer.
Se você não sabe resolvê-las não tem porque você "passar" na avaliação que imagino ser estas questões.
-
alexandre32100
-
 por edvanio1 » Qua Dez 01, 2010 00:19
por edvanio1 » Qua Dez 01, 2010 00:19
alexandre32100 escreveu:Amigo, como já foi discutido em outro tópico, este site não é um lugar onde você vai por as questões e elas vão sair resolvidas.
Se tiver alguma dúvida, posta aí.
Simplesmente por suas questões e achar que vai vir alguém resolvê-las é muito fácil, tente fazer.
Se você não sabe resolvê-las não tem porque você "passar" na avaliação que imagino ser estas questões.
Realmente nao vai ter prova ... será um trabalho de pesquisa e esse exercicio valendo 4 pontos ... essa materia é isolada no meu curso ... so tem ela de calculo ...
se puder por so as respostas agradeço msm ... obrigado ... abraço ... vlw pela atençao
-
edvanio1
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 30, 2010 03:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estatistica - Dúvida em exercício
por ffvlll » Qua Abr 06, 2011 15:43
- 0 Respostas
- 1309 Exibições
- Última mensagem por ffvlll

Qua Abr 06, 2011 15:43
Estatística
-
- Estatística - Exercício Urgente
por Carlaipb » Qua Out 05, 2011 17:12
- 1 Respostas
- 2231 Exibições
- Última mensagem por Neperiano

Qua Out 19, 2011 18:52
Estatística
-
- [exercicio de estatistica basica] URGENTE POR FAVOR
por ddesrosiers » Sex Dez 09, 2016 00:31
- 0 Respostas
- 7629 Exibições
- Última mensagem por ddesrosiers

Sex Dez 09, 2016 00:31
Estatística
-
- Desafio dos Dados
 por Molina » Dom Nov 22, 2009 13:07
por Molina » Dom Nov 22, 2009 13:07
- 5 Respostas
- 4489 Exibições
- Última mensagem por Douglasm

Seg Nov 01, 2010 19:58
Desafios Difíceis
-
- Dados não agrupados
 por jaloquingen2309+ » Ter Mar 05, 2013 01:35
por jaloquingen2309+ » Ter Mar 05, 2013 01:35
- 1 Respostas
- 1888 Exibições
- Última mensagem por jaloquingen2309+

Ter Mar 05, 2013 14:46
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 Galera preciso que me ajudem a resolver esse exercício:
Galera preciso que me ajudem a resolver esse exercício:

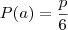 .
.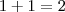 e o maior
e o maior 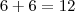 , dentre estes temos todas as possibilidades.
, dentre estes temos todas as possibilidades.




