Ja tentei de tudo ai só num sei se num soube fazer tentei distribuição binomial mais num consegui..
c alguem poder ajudar quero entender isso...



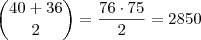 escolhas.
escolhas.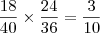
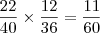
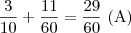

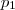 e outro com
e outro com 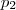 , a probabilidade de que isto aconteça é de
, a probabilidade de que isto aconteça é de  , isto explica esta parte
, isto explica esta parte.alexandre32100 escreveu:Podemos escolher:
- um rapaz de L e uma moça de A;
- uma moça de L e um rapaz de A.
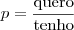 , no caso, por exemplo de escolher uma moça na turma de logística, eu tenho
, no caso, por exemplo de escolher uma moça na turma de logística, eu tenho 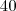 alunos, mas quero apenas as
alunos, mas quero apenas as 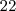 moças, portanto a probabilidade é de
moças, portanto a probabilidade é de 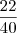 .
.alexandre32100 escreveu:No total temosescolhas.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)