ESTOU NO MEIO DE UMA INEQUAÇÃO SIMPLES MAS NÃO ENTENDO O ERRO QUE ESTOU COMETENDO. SEGUE:
(CN) Sendo m < 1 , resolva a inequação: ( x - 1 ) < x - 2.
O que tem de errado em: m(x-1)<x-2 entao mx-m<x-2 entao mx-x<m-2 entao x(m-1)<m-2 entao x<m-2/m-1?
Mas a resposta é x>m-2/m-1.
OBRIGADO!



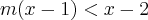

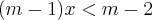
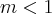 ============================>
============================> 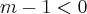 (note que esse "valor" é o mesmo que multiplica
(note que esse "valor" é o mesmo que multiplica 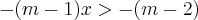
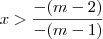
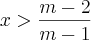
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)