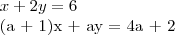
Eu sei que pelo métode de Cramer conseguiria resolvê-lo, mas minha dúvida é como faria para resolver pelo método de Rouche-Capelli.Eu até começei a fazer, assim:
p= caracteristica da matriz incompleta
q=carac. matriz completa
P/ sistema possivel e determinado:
p=q=n
p=2=q=n
Sendo assim:
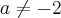
P/ sist. impossível:
Logo, p=1 e q=2
Agora, p/ p=1
a = -2 , mas para q (caracteristica matriz completa) igual a 2 tem-se
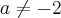
Eu devo estar fazendo alguma coisa errada, gostaria, por gentileza, que me ajudassem nessa questão.
Agradeço desde já.
por 
.
: