Uma caixa contém porcas e parafusos. Cada parafuso pesa o dobro de uma porca. O peso bruto da caixa é de 2500g e a embalagem corresponde a 4% do peso bruto. Qual a quantidade de parafusos da caixa sabendo -se que o total de peças e 100 e que cada porca pesa 20g.
parafuso = 2x20= 40
porca = 20
total peças = 100
peso bruto = 2500g
peso liquido= 2500 x 4%= 100g
Peso bruto - peso liquido = 2400
Não consigo montar uma equação pra resolver esse problema. Por favor me ajudem.
Desde ja agradeço


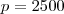
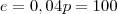
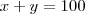
 e
e  .
. parafusos
parafusos porcas
porcas
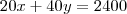
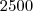
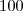


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)