por DanielFerreira » Sex Jul 06, 2012 23:18
por DanielFerreira » Sex Jul 06, 2012 23:18
Yuri,
a equação não ficou clara!
Encontrará as raízes ao colocar o

em evidência.
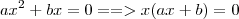

e
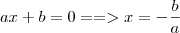
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sáb Jul 07, 2012 02:50
por MarceloFantini » Sáb Jul 07, 2012 02:50
Sua resolução foi incompleta, visto que não há condições sobre

e

para a segunda parte. Se
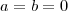
, então todo
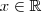
é solução. Se
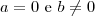
, não há solução. Se
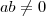
, então

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sáb Jul 07, 2012 12:27
por DanielFerreira » Sáb Jul 07, 2012 12:27
MarceloFantini escreveu:Sua resolução foi incompleta,...
Do seu ponto de vista!
A propósito, talvez não tenha notado que a equação postada pelo Yuri sofreu uma alteração.
MarceloFantini escreveu:...visto que não há condições sobre

e

para a segunda parte.
Se

, não teria sentido o título do tópico;
Como

, as duas condições descritas seriam desnecessárias;
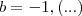
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação de 2º Grau] Incompleta
por 20nho » Sex Ago 03, 2012 21:44
- 2 Respostas
- 1828 Exibições
- Última mensagem por 20nho

Sex Ago 03, 2012 22:04
Equações
-
- [Equação 1º Grau] - Dúvida na resolução
por FernandoBasso » Qua Set 21, 2011 08:54
- 1 Respostas
- 1631 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 16:13
Álgebra Elementar
-
- [Equação 2° grau] Dúvida resolução
por brunnkpol » Ter Dez 03, 2013 17:54
- 2 Respostas
- 1652 Exibições
- Última mensagem por brunnkpol

Qua Dez 04, 2013 10:08
Equações
-
- [Equação do 2º grau] Ajuda com resolução de bhaskara
por Everton_Win » Ter Mar 26, 2013 18:36
- 2 Respostas
- 2138 Exibições
- Última mensagem por Everton_Win

Ter Mar 26, 2013 22:50
Equações
-
- [Equações do 3º grau] - Resolução
por silviopuc » Dom Dez 01, 2013 16:42
- 2 Respostas
- 1345 Exibições
- Última mensagem por silviopuc

Ter Dez 03, 2013 00:06
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

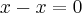


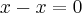

 em evidência.
em evidência.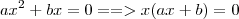

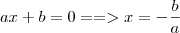

 e
e  para a segunda parte. Se
para a segunda parte. Se 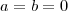 , então todo
, então todo 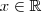 é solução. Se
é solução. Se 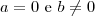 , não há solução. Se
, não há solução. Se 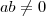 , então
, então  .
.

e
para a segunda parte.
 , não teria sentido o título do tópico;
, não teria sentido o título do tópico;  , as duas condições descritas seriam desnecessárias;
, as duas condições descritas seriam desnecessárias;