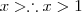por bmachado » Dom Jul 01, 2012 19:56
por bmachado » Dom Jul 01, 2012 19:56
O conjunto solução da inequação
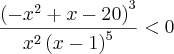
e o intervalo
Gabarito (1, infinito)
ObriGaDo pela colaboracao, poiS, eStou aprenDenDo eSSe conteuDo "Sozinho"
-
bmachado
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Fev 29, 2012 00:28
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: EF
- Andamento: formado
 por e8group » Dom Jul 01, 2012 20:49
por e8group » Dom Jul 01, 2012 20:49
bmachado ,Tudo bem ?
"Grosso modo " ...
bmachado escreveu:O conjunto solução da inequação
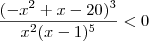
Para
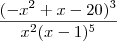
ser menor que zero tem que acontecer duas situações ,
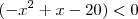
e
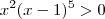
ou
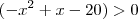
e
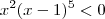
Como
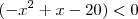
para todo x real então :
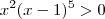
ou seja
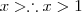
solução :
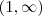
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por bmachado » Seg Jul 02, 2012 16:00
por bmachado » Seg Jul 02, 2012 16:00
santhiago escreveu:bmachado ,Tudo bem ?
"Grosso modo " ...
bmachado escreveu:O conjunto solução da inequação
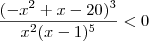
Para
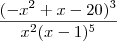
ser menor que zero tem que acontecer duas situações ,
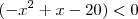
e
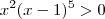
ou
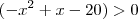
e
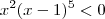
Como
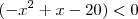
para todo x real então :
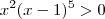
ou seja
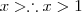
ObriGaDo, acHei q teria q reSolver oS parenteSeS
solução :
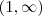
-
bmachado
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Fev 29, 2012 00:28
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: EF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6323 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7396 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3738 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2119 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1627 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
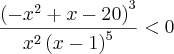 e o intervalo
e o intervalo
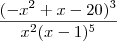 ser menor que zero tem que acontecer duas situações ,
ser menor que zero tem que acontecer duas situações ,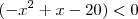 e
e 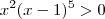 ou
ou 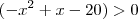 e
e 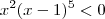
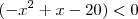 para todo x real então :
para todo x real então :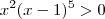 ou seja
ou seja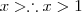
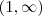

ser menor que zero tem que acontecer duas situações ,
e
ou
e
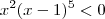
para todo x real então :
ou seja