Estou fazendo outro exercicio de % mas não deu certo :
Dois levantamentos sobre o número de alunos ingressantes em uma instituição com objetivo de acompanhar o índice de desistência nos cursos :um na metade do semestre e outro no final do semestre letivo.
No 1º levantamento constatou que 10% dos alunos ingressantes naquele semestre haviam desistidos dos cursos
No 2º levantamento constatou que 5% dos alunos que estavam cursando na ocasião do 1º levantamento tinham desistido dos cursos.Tendo como base o número de alunos ingressantes naquele semestre letivo, o índice de desistência nos cursos dessea instituição, no referido semestre : resposta 14,5%
minha tentativa
1º levantamento 10-100=90 é número de alunos ingressantes naquele semestre letivo
2ºlevantamento 5*90=45 é número desistência nos cursos
90/45 = 2%


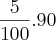 =
=


 , avisa que eu resolvo.
, avisa que eu resolvo.

