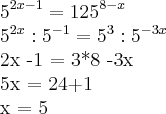
Acredito estar certa, mas se alguém puder fazer alguma análise!
=============================
![\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35} \sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35}](/latexrender/pictures/faf317b98ffaeb2e05d768891fa32b24.png)
Sinceramente, nesta segunda equação, não consigo passar daí!

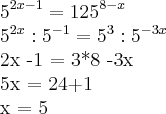
![\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35} \sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35}](/latexrender/pictures/faf317b98ffaeb2e05d768891fa32b24.png)

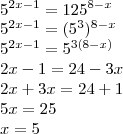
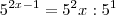 ... o 1 é positivo, pois:
... o 1 é positivo, pois: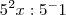
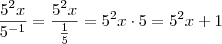
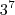
![\\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5} \\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5}](/latexrender/pictures/4b702bafd63c83d08ec55896ef4be200.png)
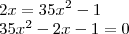
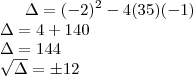
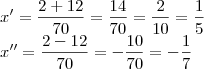


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)