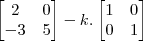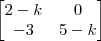por tonnis9 » Qua Out 24, 2012 11:35
Considere a matriz M (a matriz está na figura em anexo)
a) Construa a matriz M -kI, sendo k E R e I a matriz identidade 2x2
b) Quais os valores de k que tornam nulo o determinante da matriz M-kI?
Não sei o que eu faço com esse 'k'
- Anexos
-
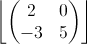
- matriz
- CodeCogsEqn.png (790 Bytes) Exibido 2777 vezes
-
tonnis9
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qua Out 24, 2012 00:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por young_jedi » Qua Out 24, 2012 17:02
a) monte a equação utilizando aquilo que o exercicio forneceu
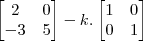
fazendo a multiplicação e a soma de matrizes
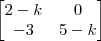
para o item b uso o calculo do determinante e igule a 0 para encontrar o k
Obs: quando for postar matrizes utilize o Latex, em caso de duvida veja este
topico de dicas pode ajudar
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
