 por Anninha » Qui Mar 28, 2013 22:44
por Anninha » Qui Mar 28, 2013 22:44
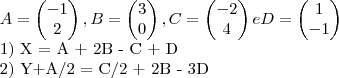
Alguém estaria disposto a me ensinar como resolver?
-
Anninha
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 22:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Mar 29, 2013 00:56
por DanielFerreira » Sex Mar 29, 2013 00:56
Olá
Anninha,
seja bem-vinda ao fórum!
Antes de respondê-la, devo informá-la o quão é importante a objetividade no
Título do seu tópico. Evite expressões desse tipo: Help, socorro, ajuda urgente,...
Segue a resolução do item 1):
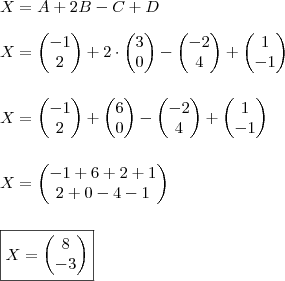
Quanto ao item 2), a resolução é análoga. Tente concluir, caso contrário retorne!
Atentamente,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Anninha » Sex Mar 29, 2013 12:22
por Anninha » Sex Mar 29, 2013 12:22
Daniel, eu tentei fazer, e o resultado do primeiro deu o mesmo valor. Mas, a segunda questão eu tentei fazer, mas não sei como concluir. Poderia me ensinar como faze-la?
Como fiz:
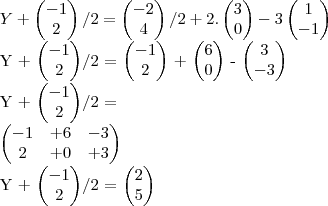
(obs: Não sei como colocar divisão no editor de fórmulas)
E quando chega aqui, não sei como resolver e não sei se está correto, poderia me ajudar ?
-
Anninha
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 22:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Mar 29, 2013 12:53
por e8group » Sex Mar 29, 2013 12:53
Percebo que você tem dificuldade com operações com matrizes (neste caso matriz coluna ) ,por este motivo
vou indicar a seguinte vídeo aula sobre matrizes , disponível em :
http://www.youtube.com/watch?v=sw18GQES ... c5HCIz2Z5D Seria muito importante tomar nota das videos aulas ,principalmente sobre operações com matrizes .Poderia associar também as vídeos aulas uma sequência de exercício resolvidos com respeito a operações entre matrizes(que pode encontrar em livros e internet) e tenta desenvolvê- los e comparar sua resolução com a solução proposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Anninha » Sex Mar 29, 2013 14:20
por Anninha » Sex Mar 29, 2013 14:20
santhiago escreveu:Percebo que você tem dificuldade com operações com matrizes (neste caso matriz coluna ) ,por este motivo
vou indicar a seguinte vídeo aula sobre matrizes , disponível em :
http://www.youtube.com/watch?v=sw18GQES ... c5HCIz2Z5D Seria muito importante tomar nota das videos aulas ,principalmente sobre operações com matrizes .Poderia associar também as vídeos aulas uma sequência de exercício resolvidos com respeito a operações entre matrizes(que pode encontrar em livros e internet) e tenta desenvolvê- los e comparar sua resolução com a solução proposta .
Santhiago, eu já vi todos esses videos de matrizes. E estou tentando resolver este exercício. (Estou fazendo isto por conta própria, meu professor de matemática ainda não passou este assunto). Eu o resolvi, mas não sei se esta correto, e gostaria de comparar com outros resultados. Se puder ajudar eu agradeço.
-
Anninha
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 22:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Mar 29, 2013 15:18
por DanielFerreira » Sex Mar 29, 2013 15:18
Oi
Anninha,
Para fazer

utiliza-se o seguinte código:
- Código: Selecionar todos
\frac{1}{2}
Segue a resolução do item 2):
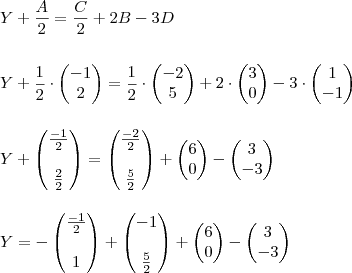
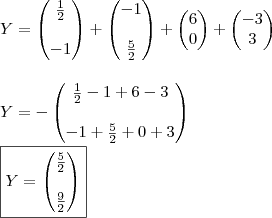
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Anninha » Sex Mar 29, 2013 15:52
por Anninha » Sex Mar 29, 2013 15:52
Daniel, muito obrigada. Mas você entendeu errado porque eu não soube usar corretamente o editor de fórmulas, é assim:

Que fica:
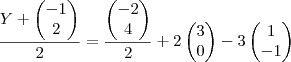
Poderia me ajudar, se não for muito incomodo.
-
Anninha
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 22:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


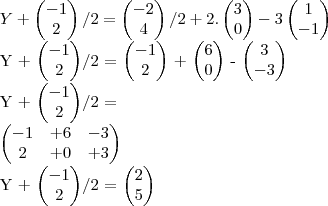



 utiliza-se o seguinte código:
utiliza-se o seguinte código: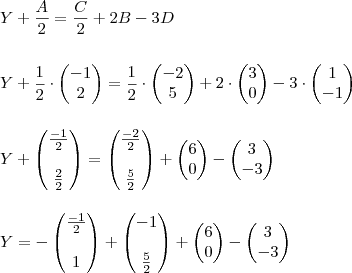
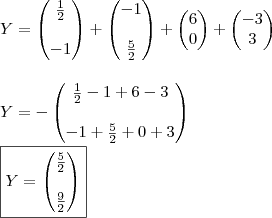


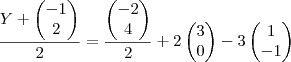



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.