Sejam A, B e C matrizes quadradas de ordem 3 e O a
matriz nula também de ordem 3. Assinale a alternativa
correta:
a) Se A . B = O, então: A = O ou B = O =>>>>>> falsa!
Pessoal, as outras opções eu não coloquei porque entendi porquê estavam correta, mas essa alternativa eu não consigo entender porquê está errada.
Obrigada
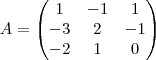e 
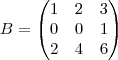matrizes 3x3.
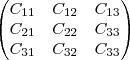
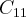: 1.1 + (-1).0 + (1).2 = 3
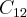: 1.2+(-1).0+1.4= 6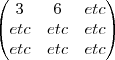
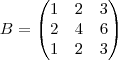
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)